Advertisements
Advertisements
प्रश्न
A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36 t + 0.018 x + π/4)
Where x and y are in cm and t in s. The positive direction of x is from left to right.
(a) Is this a travelling wave or a stationary wave?
If it is travelling, what are the speed and direction of its propagation?
(b) What are its amplitude and frequency?
(c) What is the initial phase at the origin?
(d) What is the least distance between two successive crests in the wave?
Advertisements
उत्तर १
(a) Yes; Speed = 20 m/s, Direction = Right to left
(b) 3 cm; 5.73 Hz
(c) `pi/4`
(d) 3.49 m
Explanation:
(a) The equation of a progressive wave travelling from right to left is given by the displacement function:
y (x, t) = a sin (ωt + kx + Φ) … (i)
The given equation is:
`y(x,t) = 3.0 sin (36t + 0.018 x + pi/4)` ...(ii)
On comparing both the equations, we find that equation (ii) represents a travelling wave, propagating from right to left.
Now, using equations (i) and (ii), we can write:
ω = 36 rad/s and k = 0.018 m–1
We know that:
`v = omega/(2pi)` and `lambda = (2pi)/k`
Also
= νλ
`:. v = (omega/2pi) xx ((2pi)/k) = omega/k`
`= 36/0.018 = 2000 "cm/s" = 20 "m/s"`
Hence, the speed of the given travelling wave is 20 m/s.
b) Amplitude of the given wave, a = 3 cm
Frequency of the given wave:
`v =omega/(2pi) = 36/(2xx3.14)= 5.73 "Hz"`
(c) On comparing equations (i) and (ii), we find that the initial phase angle, `phi = pi/4`
(d) The distance between two successive crests or troughs is equal to the wavelength of the wave.
Wavelength is given by the relation: k = `(2pi)/lambda`
`:. lambda = (2pi)/k = (2xx3.14)/(0.018) = 348.89 cm = 3.49 m`
उत्तर २
The given equation is y(x,t) = `3.0 sin (36t + 0.018x + pi/4)` , where x and y are in cm and t in s.
a) The equation is the equation of a travelling wave, travelling from right to left (i.e along -ve direction of x because it is an equation of the type )
`y(x,t) = A sin(omegat + kx + phi)`
Here A = 3.0 cm, `omega = 36 "rad s"^(-1)`, k = 0.018 cm and `phi = pi/4`
:. Speed of wave propagation,
`v = omega/k = (36 " rad s"^(-1))/(0.018 cm^(-1)) = (36 "rad s"^(-1))/(0.018 xx 10^2 "ms^(-1)) = 20 ms^(-1)`
b) Amplitude of wave, A = 3.0 cm = 0.03 m
Frequency of wave `v = omega/(2pi) = 36/(2pi) = 5.7` Hz
c) Initial phase at the origin, `phi = pi/4`
d) Least distance between two successive crests in the wave
`= lambda = (2pi)/k = (2pi)/0.018`
= 349 cm = 3.5 m
संबंधित प्रश्न
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = cos x sin t + cos 2x sin 2t
Explain why (or how): Bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,
Explain why (or how) Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases
A transverse wave travels along the Z-axis. The particles of the medium must move
A wave going in a solid
(a) must be longitudinal
(b) may be longitudinal
(c) must be transverse
(d) may be transverse.
A wave moving in a gas
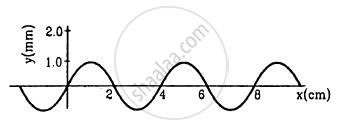
Figure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20 cm s−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
A vertical rod is hit at one end. What kind of wave propagates in the rod if (a) the hit is made vertically (b) the hit is made horizontally?
Two blocks each having a mass of 3⋅2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB (See following figure). The linear mass density of the wire AB is 10 g m−1 and that of CD is 8 g m−1. Find the speed of a transverse wave pulse produced in AB and CD.
An organ pipe, open at both ends, contains
In the arrangement shown in figure , the string has a mass of 4⋅5 g. How much time will it take for a transverse disturbance produced at the floor to reach the pulley? Take g = 10 m s−2.
A circular loop of string rotates about its axis on a frictionless horizontal place at a uniform rate so that the tangential speed of any particle of the string is ν. If a small transverse disturbance is produced at a point of the loop, with what speed (relative to the string) will this disturbance travel on the string?
A wire, fixed at both ends is seen to vibrate at a resonant frequency of 240 Hz and also at 320 Hz. (a) What could be the maximum value of the fundamental frequency? (b) If transverse waves can travel on this string at a speed of 40 m s−1, what is its length?
A 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220 m s−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0⋅5 cm, write a suitable equation describing the motion.
Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies? (c) Which overtones are these frequencies? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string?
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = 2 cos (3x) sin (10t)
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
`"y" = 2sqrt(x - "vt")`
