Advertisements
Advertisements
प्रश्न
For the wave described in Exercise 15.8, plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in travelling wave differ from one point to another: amplitude, frequency or phase?
उत्तर १
All the waves have different phases.
The given transverse harmonic wave is:
`y (x,t)= 3.0 sin (36t + 0.018x + pi/4)` ...(i)
For x = 0, the equation reduces to:
`y (0,t) = 3.0 sin (36t + pi/4)`
Also, `omega = (2pi)/T = 36 " rad/s"^(-1)`
`:. T = pi/8 s`
Now, plotting y vs. t graphs using the different values of t, as listed in the given table.
| t(s) | 0 | T/8 | 2T/8 | 3T/8 | 4T/8 | 5T/8 | 6T/8 | 7T/8 |
| y(cm) | `(3sqrt2)/2` | 3 | `(3sqrt2)/2` | 0 | `(-3sqrt2)/2` | -3 | `(-3sqrt2)/2` | 0 |
For x = 0, x = 2, and x = 4, the phases of the three waves will get changed. This is because amplitude and frequency are invariant for any change in x. The y-t plots of the three waves are shown in the given figure.
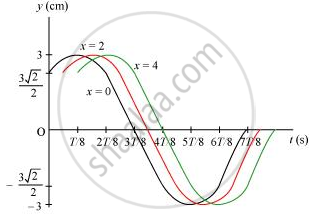
उत्तर २
The transverse harmonic wave is
`y(x,t) = 3.0 sin (36t + 0.018x + pi/4)`
for x = 0
`y(0,t) = 3 sin(36t + 0 + pi/4) = 3 sin (36t + pi/4)` ...1
Here `omega = (2pi)/T = 36 => T =(2pi)/36`
To plot a(y) versus (t) graph, different values of y corresponding to the values of t may be tabulated as under (by making use of equation 1)
| t(s) | 0 | T/8 | 2T/8 | 3T/8 | 4T/8 | 5T/8 | 6T/8 | 7T/8 | T |
| y(cm) | `(3sqrt2)/2` | 3 | `(3sqrt2)/2` | 0 | `(-3sqrt2)/2` | -3 | `(-3sqrt2)/2` | 0 | `3/sqrt2` |
Using the values of t and y (as in the table), a graph is plotted as under The graph obtained is sinusoidal.
Similar graphs are obtained for y x = 2 cm and x = 4 cm. The (incm) oscillatory motion in the travelling wave only differs in respect of phase. Amplitude and frequency of oscillatory motion remains the same in all the cases.
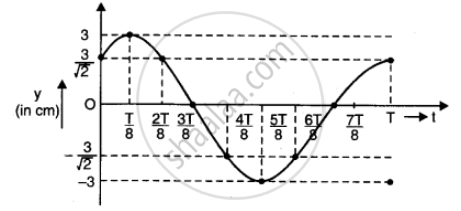
APPEARS IN
संबंधित प्रश्न
(i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
Two waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
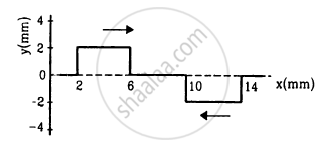
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
A wire of length 2⋅00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
A steel wire fixed at both ends has a fundamental frequency of 200 Hz. A person can hear sound of maximum frequency 14 kHz. What is the highest harmonic that can be played on this string which is audible to the person?
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
The amplitude of wave disturbance propagating in the positive x-direction given is by `1/(1 + x)^2` at time t = 0 and `1/(1 + (x - 2)^2)` at t = 1 s, where x and y are in 2 metres. The shape of wave does not change during the propagation. The velocity of the wave will be ______ m/s.
