Advertisements
Advertisements
Question
For the wave described in Exercise 15.8, plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in travelling wave differ from one point to another: amplitude, frequency or phase?
Advertisements
Solution 1
All the waves have different phases.
The given transverse harmonic wave is:
`y (x,t)= 3.0 sin (36t + 0.018x + pi/4)` ...(i)
For x = 0, the equation reduces to:
`y (0,t) = 3.0 sin (36t + pi/4)`
Also, `omega = (2pi)/T = 36 " rad/s"^(-1)`
`:. T = pi/8 s`
Now, plotting y vs. t graphs using the different values of t, as listed in the given table.
| t(s) | 0 | T/8 | 2T/8 | 3T/8 | 4T/8 | 5T/8 | 6T/8 | 7T/8 |
| y(cm) | `(3sqrt2)/2` | 3 | `(3sqrt2)/2` | 0 | `(-3sqrt2)/2` | -3 | `(-3sqrt2)/2` | 0 |
For x = 0, x = 2, and x = 4, the phases of the three waves will get changed. This is because amplitude and frequency are invariant for any change in x. The y-t plots of the three waves are shown in the given figure.
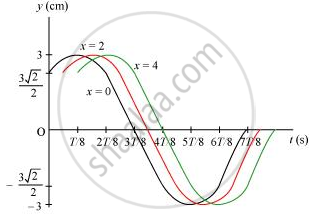
Solution 2
The transverse harmonic wave is
`y(x,t) = 3.0 sin (36t + 0.018x + pi/4)`
for x = 0
`y(0,t) = 3 sin(36t + 0 + pi/4) = 3 sin (36t + pi/4)` ...1
Here `omega = (2pi)/T = 36 => T =(2pi)/36`
To plot a(y) versus (t) graph, different values of y corresponding to the values of t may be tabulated as under (by making use of equation 1)
| t(s) | 0 | T/8 | 2T/8 | 3T/8 | 4T/8 | 5T/8 | 6T/8 | 7T/8 | T |
| y(cm) | `(3sqrt2)/2` | 3 | `(3sqrt2)/2` | 0 | `(-3sqrt2)/2` | -3 | `(-3sqrt2)/2` | 0 | `3/sqrt2` |
Using the values of t and y (as in the table), a graph is plotted as under The graph obtained is sinusoidal.
Similar graphs are obtained for y x = 2 cm and x = 4 cm. The (incm) oscillatory motion in the travelling wave only differs in respect of phase. Amplitude and frequency of oscillatory motion remains the same in all the cases.
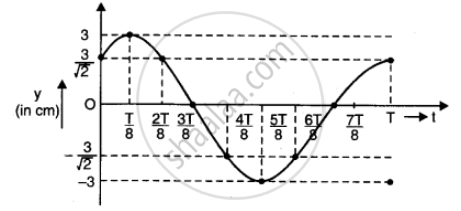
APPEARS IN
RELATED QUESTIONS
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
A SONAR system fixed in a submarine operates at a frequency 40.0 kHz. An enemy submarine moves towards the SONAR with a speed of 360 km h–1. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 1450 m s–1.
Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of S wave is about 4.0 km s–1, and that of P wave is 8.0 km s–1. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in straight line, at what distance does the earthquake occur?
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
A sine wave is travelling in a medium. A particular particle has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
A wave pulse, travelling on a two-piece string, gets partially reflected and partially transmitted at the junction. The reflected wave is inverted in shape as compared to the incident one. If the incident wave has wavelength λ and the transmitted wave λ'
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N m−1 and is stretched by 1⋅0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
A wire of length 2⋅00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
Given below are some functions of x and t to represent the displacement of an elastic wave.
- y = 5 cos (4x) sin (20t)
- y = 4 sin (5x – t/2) + 3 cos (5x – t/2)
- y = 10 cos [(252 – 250) πt] cos [(252 + 250)πt]
- y = 100 cos (100πt + 0.5x)
State which of these represent
- a travelling wave along –x direction
- a stationary wave
- beats
- a travelling wave along +x direction.
Given reasons for your answers.
A wave of frequency υ = 1000 Hz, propagates at a velocity v = 700 m/sec along x-axis. Phase difference at a given point x during a time interval M = 0.5 × 10-3 sec is ______.
