Advertisements
Advertisements
Question
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
Solution
Given,
Equation of the wave,
\[y = \left( 0 . 10 \text{ mm } \right) \sin\left( 31 . 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right) t\]
The general equation is \[y = A\sin\left\{ \left( \frac{2\pi x}{\lambda} \right) + \omega t \right\}\]
From the above equation, we can conclude:
(a) The wave is travelling in the negative x-direction.
(b) \[\frac{2\pi}{\lambda} = 31 . 4 m^{- 1}\]
\[\Rightarrow \lambda = \frac{2\pi}{31 . 4} = 0 . 2 m = 20 cm\]
And,
\[\omega = 314 s^{- 1} \]
\[ \Rightarrow 2\pi f = 314\]
\[ \Rightarrow f = \frac{314}{2\pi}\]
\[= \frac{314}{2 \times 3 . 14}\]
\[= 50 s^{- 1} = 50 Hz\]
Wave speed:
\[\nu = \lambda f = 20 \times 50\]
\[=1000 cm/s\]
(c) Maximum displacement, A = 0.10 mm
Maximum velocity = \[a\omega = 0 . 1 \times {10}^{- 1} \times 314\]
= 3.14 cm/s
APPEARS IN
RELATED QUESTIONS
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the transmitted sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
For the wave described in Exercise 15.8, plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in travelling wave differ from one point to another: amplitude, frequency or phase?
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m s–1, (b) recedes from the platform with a speed of 10 m s–1? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 m s–1.
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
Two waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
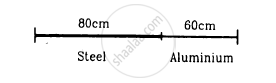
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
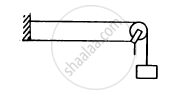
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
A man standing unsymmetrical position between two mountains and fires a gun. He hears the first echo after 1.5 s and the second echo after 2.5 s. If the speed of sound in air is 340 m/s, then the distance between the mountains will be ______
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air is independent of pressure.
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
Speed of sound wave in air ______.
A string of mass 2.5 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in ______.
