Advertisements
Advertisements
Question
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
Solution
Given,
Wave velocity = \[\nu\]
Shape of the string at
\[t = t_0\]
\[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]
For a wave travelling in the positive x-direction, the general equation is given by \[y = A \sin \left( \frac{x}{a} - \frac{t}{T} \right)\]
Putting t = − t and comparing with equation (i), we get:
\[g\left( x, 0 \right) = A\sin\left\{ \left( \frac{x}{a} \right) + \left( \frac{t_0}{T} \right) \right\}\]
\[ \Rightarrow g\left( x, t \right) = A\sin\left[ \left\{ \left( \frac{x}{a} \right) + \frac{t_0}{T} \right\} - \left( \frac{t}{T} \right) \right]\]
\[Now, \]
\[T = \frac{a}{\nu}\]
\[Here, \]
a = Wave length
nu = Velocity of the wave
Thus, we have:
\[y = A\sin \left[ \left( \frac{x}{a} \right) + \frac{t_0}{\left( \frac{a}{\nu} \right)} - \frac{t}{\left( \frac{a}{\nu} \right)} \right]\]
\[\Rightarrow y = A\sin \frac{x + \nu \left( t_0 - t \right)}{a}\]
APPEARS IN
RELATED QUESTIONS
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
Choose the correct option:
Which of the following equations represents a wave travelling along Y-axis?
A wave pulse, travelling on a two-piece string, gets partially reflected and partially transmitted at the junction. The reflected wave is inverted in shape as compared to the incident one. If the incident wave has wavelength λ and the transmitted wave λ'
Two wires A and B, having identical geometrical construction, are stretched from their natural length by small but equal amount. The Young modules of the wires are YA and YB whereas the densities are \[\rho_A \text{ and } \rho_B\]. It is given that YA > YB and \[\rho_A > \rho_B\]. A transverse signal started at one end takes a time t1 to reach the other end for A and t2 for B.
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave? (b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N m−1 and is stretched by 1⋅0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
Two long strings A and B, each having linear mass density
\[1 \cdot 2 \times {10}^{- 2} kg m^{- 1}\] , are stretched by different tensions 4⋅8 N and 7⋅5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A?
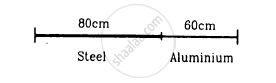
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
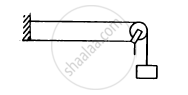
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m.
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
The amplitude of wave disturbance propagating in the positive x-direction given is by `1/(1 + x)^2` at time t = 0 and `1/(1 + (x - 2)^2)` at t = 1 s, where x and y are in 2 metres. The shape of wave does not change during the propagation. The velocity of the wave will be ______ m/s.
An engine is approaching a cliff at a constant speed. When it is at a distance of 0.9 km from cliff it sounds a whistle. The echo of the sound is heard by the driver after 5 seconds. Velocity of sound in air is equal to 330 ms-1. The speed of the engine is ______ km/h.
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
