Advertisements
Advertisements
Question
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
Solution 1
Equation for a travelling harmonic wave is given as:
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
= 2.0 cos (20πt – 0.016πx + 0.70 π)
Where,
Propagation constant, k = 0.0160 π
Amplitude, a = 2 cm
Angular frequency, ω= 20 π rad/s
Phase difference is given by the relation:
`phi = kx = (2pi)/lambda`
For `x = (3lambda)/4`
`phi = (2pi)/lambda xx (3lambda)/4`
`= 1.5 pi` rad
Solution 2
The given equation can be drawn be rewritten as under
y(x, t) `= 2.0 cos [2pi (10"t" - 0.0080x) + 2pi xx 0.35]`
or y(x, t) `= 2.0 cos [2pi xx 0.0080((10"t")/0.0080 - x) + 0.7pi]`
Comparing this equation with the standard equation of a travelling harmonic wave.
`(2pi)/lambda = 2pi xx 0.0080` or `lambda = 1/0.0080 "cm" = 125` cm
The phase difference between oscillatory motion of two points seperated by a distance `trianglex` is given by
`trianglephi = (2pi)/lambda trianglex`
When `trianglex = (3lambda)/4 = (3xx125)/4` cm, then
`triangle phi = (2phi)/125 xx (3xx125)/4`
`= (3pi)/2 "rad"`
APPEARS IN
RELATED QUESTIONS
(i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
Velocity of sound in air is 332 m s−1. Its velocity in vacuum will be
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A wave travels along the positive x-direction with a speed of 20 m s−1. The amplitude of the wave is 0⋅20 cm and the wavelength 2⋅0 cm. (a) Write the suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x= 2⋅0 cm at time t = 0 according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?
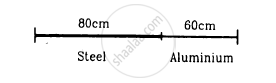
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
A steel wire has a length of 12 m and a mass of 2.10 kg. What will be the speed of a transverse wave on this wire when a tension of 2.06 × 104N is applied?
The displacement y of a particle in a medium can be expressed as, y = `10^-6sin(100t + 20x + pi/4)` m where t is in second and x in meter. The speed of the wave is ______.
