Advertisements
Advertisements
प्रश्न
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
उत्तर १
Equation for a travelling harmonic wave is given as:
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
= 2.0 cos (20πt – 0.016πx + 0.70 π)
Where,
Propagation constant, k = 0.0160 π
Amplitude, a = 2 cm
Angular frequency, ω= 20 π rad/s
Phase difference is given by the relation:
`phi = kx = (2pi)/lambda`
For `x = (3lambda)/4`
`phi = (2pi)/lambda xx (3lambda)/4`
`= 1.5 pi` rad
उत्तर २
The given equation can be drawn be rewritten as under
y(x, t) `= 2.0 cos [2pi (10"t" - 0.0080x) + 2pi xx 0.35]`
or y(x, t) `= 2.0 cos [2pi xx 0.0080((10"t")/0.0080 - x) + 0.7pi]`
Comparing this equation with the standard equation of a travelling harmonic wave.
`(2pi)/lambda = 2pi xx 0.0080` or `lambda = 1/0.0080 "cm" = 125` cm
The phase difference between oscillatory motion of two points seperated by a distance `trianglex` is given by
`trianglephi = (2pi)/lambda trianglex`
When `trianglex = (3lambda)/4 = (3xx125)/4` cm, then
`triangle phi = (2phi)/125 xx (3xx125)/4`
`= (3pi)/2 "rad"`
APPEARS IN
संबंधित प्रश्न
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will ______.
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
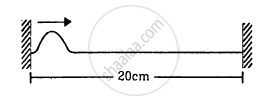
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
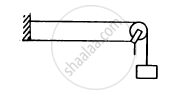
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36t + 0.018x + π/4) where x and y are in cm and t is in s. The positive direction of x is from left to right.
- The wave is travelling from right to left.
- The speed of the wave is 20 m/s.
- Frequency of the wave is 5.7 Hz.
- The least distance between two successive crests in the wave is 2.5 cm.
