Advertisements
Advertisements
प्रश्न
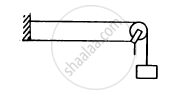
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
Advertisements
उत्तर
Density of the block = ρ
Volume of block = V
∴ Weight of the block is, W = ρVg
∴ Tension in the string, T = W
The tuning fork resonates with different frequencies in the two cases.
Let the tenth harmonic be f10.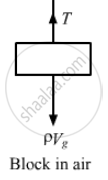
\[f_{11} = \frac{11}{2L}\sqrt{\frac{T'}{m}}\]
\[ = \frac{11}{2L}\sqrt{\frac{\left( \rho - \rho_w \right) Vg}{m}}\]
The frequency (f) of the tuning fork is same.
\[\therefore f_{10} = f_{11} \]
\[ \Rightarrow \frac{10}{2L}\sqrt{\frac{\rho Vg}{m}} = \frac{11}{2L}\sqrt{\frac{\left( \rho - \rho_\omega \right) Vg}{m}}\]
\[ \Rightarrow \frac{100}{121} = \frac{\rho - 1}{\rho} \left( because \rho_\omega = 1 gm/cc \right)\]
\[ \Rightarrow 100 \rho = 121 \rho - 121\]
\[ \Rightarrow \rho = \frac{121}{21} = 5 . 8 gm/cc\]
\[= 5 . 8 \times {10}^3 kg/ m^3\]
Therefore, the required density is \[5 . 8 \times {10}^3 kg/ m^3\]
APPEARS IN
संबंधित प्रश्न
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
Two long strings A and B, each having linear mass density
\[1 \cdot 2 \times {10}^{- 2} kg m^{- 1}\] , are stretched by different tensions 4⋅8 N and 7⋅5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A?
A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g m−1 kept under a tension of 60 N. (a) Find the average power transmitted across a given point on the string. (b) Find the total energy associated with the wave in a 2⋅0 m long portion of the string.
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air is independent of pressure.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
The amplitude of wave disturbance propagating in the positive x-direction given is by `1/(1 + x)^2` at time t = 0 and `1/(1 + (x - 2)^2)` at t = 1 s, where x and y are in 2 metres. The shape of wave does not change during the propagation. The velocity of the wave will be ______ m/s.
