Advertisements
Advertisements
Question
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
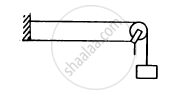
Solution
Density of the block = ρ
Volume of block = V
∴ Weight of the block is, W = ρVg
∴ Tension in the string, T = W
The tuning fork resonates with different frequencies in the two cases.
Let the tenth harmonic be f10.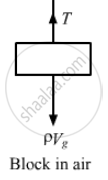
\[f_{11} = \frac{11}{2L}\sqrt{\frac{T'}{m}}\]
\[ = \frac{11}{2L}\sqrt{\frac{\left( \rho - \rho_w \right) Vg}{m}}\]
The frequency (f) of the tuning fork is same.
\[\therefore f_{10} = f_{11} \]
\[ \Rightarrow \frac{10}{2L}\sqrt{\frac{\rho Vg}{m}} = \frac{11}{2L}\sqrt{\frac{\left( \rho - \rho_\omega \right) Vg}{m}}\]
\[ \Rightarrow \frac{100}{121} = \frac{\rho - 1}{\rho} \left( because \rho_\omega = 1 gm/cc \right)\]
\[ \Rightarrow 100 \rho = 121 \rho - 121\]
\[ \Rightarrow \rho = \frac{121}{21} = 5 . 8 gm/cc\]
\[= 5 . 8 \times {10}^3 kg/ m^3\]
Therefore, the required density is \[5 . 8 \times {10}^3 kg/ m^3\]
APPEARS IN
RELATED QUESTIONS
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the transmitted sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1? The operating frequency of the scanner is 4.2 MHz.
(i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
Choose the correct option:
Which of the following equations represents a wave travelling along Y-axis?
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
Two long strings A and B, each having linear mass density
\[1 \cdot 2 \times {10}^{- 2} kg m^{- 1}\] , are stretched by different tensions 4⋅8 N and 7⋅5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A?
A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g m−1 kept under a tension of 60 N. (a) Find the average power transmitted across a given point on the string. (b) Find the total energy associated with the wave in a 2⋅0 m long portion of the string.
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
A steel wire fixed at both ends has a fundamental frequency of 200 Hz. A person can hear sound of maximum frequency 14 kHz. What is the highest harmonic that can be played on this string which is audible to the person?
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
A man standing unsymmetrical position between two mountains and fires a gun. He hears the first echo after 1.5 s and the second echo after 2.5 s. If the speed of sound in air is 340 m/s, then the distance between the mountains will be ______
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36t + 0.018x + π/4) where x and y are in cm and t is in s. The positive direction of x is from left to right.
- The wave is travelling from right to left.
- The speed of the wave is 20 m/s.
- Frequency of the wave is 5.7 Hz.
- The least distance between two successive crests in the wave is 2.5 cm.
Speed of sound waves in a fluid depends upon ______.
- directty on density of the medium.
- square of Bulk modulus of the medium.
- inversly on the square root of density.
- directly on the square root of bulk modulus of the medium.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
