Advertisements
Advertisements
Question
(i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
Solution 1
(i) For the wave on the string described in questions we have seen that l = 1.5 m and λ = 3 m. So, it is clear that λ = λ /2 and for a string clamped at both ends, it is possible only when both ends behave as nodes and there is only one antinode in between i.e., whole string is vibrating in one segment only.
(a) Yes, all the sring particles, except nodes, vibrate with the same frequency v = 60 Hz.
(b) As all string particles lie in one segment, all of them are in same phase.
(c) Amplitude varies from particle to particle. At antinode, amplitude = 2A = 0.06 m. It gradually falls on going towards nodes and at nodes, and at nodes, it is zero.
(ii) Amplitude at a point x = 0.375 m will be obtained by putting cos (120 πt) as + 1 in the wave equation.
`:. A(x) = 0.06 sin((2pi)/3 xx 0.375) xx 1 = 0.06 sin pi/4= 0.042 m`
Solution 2
(i)
(a) Yes, except at the nodes
(b) Yes, except at the nodes
(c) No
(ii) 0.042 m
Explanation:
(i)
(a) All the points on the string oscillate with the same frequency, except at the nodes which have zero frequency.
(b) All the points in any vibrating loop have the same phase, except at the nodes.
(c) All the points in any vibrating loop have different amplitudes of vibration.
(ii) The given equation is:
`y(x,t) = 0.06 sin ((2pi)/3 x) cos(120 pi t)`
For x = 0.375 m and t = 0
Amplitude = Displacement = `0.06 sin((2pi)/3 x)cos 0`
`= 0.06 sin (2pi/3 xx 0.375) xx 1`
`= 0.06 sin (0.25 pi) = 0.06 sin (pi/4)`
`= 0.06 xx 1/sqrt2 = 0.042 m`
APPEARS IN
RELATED QUESTIONS
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
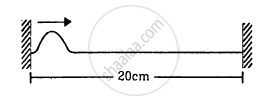
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
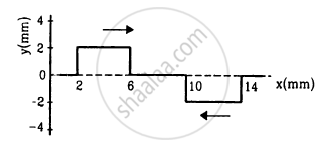
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4 cm \right) \sin\left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
A man standing unsymmetrical position between two mountains and fires a gun. He hears the first echo after 1.5 s and the second echo after 2.5 s. If the speed of sound in air is 340 m/s, then the distance between the mountains will be ______
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
The displacement y of a particle in a medium can be expressed as, y = `10^-6sin(100t + 20x + pi/4)` m where t is in second and x in meter. The speed of the wave is ______.
