Advertisements
Advertisements
Question
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
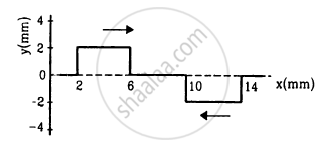
Solution
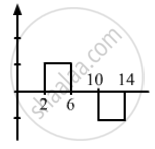
Given,
Speed of the wave pulse travelling in the opposite direction, v = 50 cm s−1 = 500 mm s−1
Distances travelled by the pulses:
Using s = vt, we get:
\[In t = 4 ms = 4 \times {10}^{- 3} s, \]
\[s = \nu t = 500 \times 4 \times {10}^{- 3} = 2 mm . \]
\[In t = 6 ms = 6 \times {10}^{- 3} s, \]
\[s = 500 \times 6 \times {10}^{- 3} = 3 mm . \]
\[In t = 8 ms = 8 \times {10}^{- 3} s, \]
\[s = \nu t = 500 \times 8 \times {10}^{- 3} = 4 mm . \]
\[In t = 12 ms = 12 \times {10}^{- 3} s, \]
\[s = 500 \times 12 \times {10}^{- 3} = 6 mm .\]
The shapes of the string at different times are shown in the above.
APPEARS IN
RELATED QUESTIONS
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
Two wires A and B, having identical geometrical construction, are stretched from their natural length by small but equal amount. The Young modules of the wires are YA and YB whereas the densities are \[\rho_A \text{ and } \rho_B\]. It is given that YA > YB and \[\rho_A > \rho_B\]. A transverse signal started at one end takes a time t1 to reach the other end for A and t2 for B.
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
Two waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
A sonometer wire supports a 4 kg load and vibrates in fundamental mode with a tuning fork of frequency 416. Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
A wave travels along the positive x-direction with a speed of 20 m s−1. The amplitude of the wave is 0⋅20 cm and the wavelength 2⋅0 cm. (a) Write the suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x= 2⋅0 cm at time t = 0 according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N m−1 and is stretched by 1⋅0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
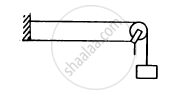
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
A 2⋅00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
What is the interference of sound waves?
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
