Advertisements
Advertisements
Question
A wave travels along the positive x-direction with a speed of 20 m s−1. The amplitude of the wave is 0⋅20 cm and the wavelength 2⋅0 cm. (a) Write the suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x= 2⋅0 cm at time t = 0 according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?
Solution
A wave travels along the positive x-direction.
Wave amplitude (A) = 0.20 cm
Wavelength (λ) = 20 cm
Wave speed (v) = 20 m/s
(a) General wave equation along the x-axis:
\[y = A\sin\left( kx - \omega \right)\]
\[ \therefore k = \frac{2\pi}{\lambda} = \frac{2\pi}{2} = \pi {cm}^{- 1} \]
\[T = \frac{\lambda}{\nu} = \frac{2}{2000}\]
\[ = \frac{1}{1000} = {10}^{- 3} s\]
\[\omega = \frac{2\pi}{T} = 2\pi \times {10}^3 s^{- 1}\]
Wave equation:
\[y = \left( 0 . 2 cm \right) \sin\left[ \left( \pi {cm}^{- 1} \right) x - \left( 2\pi \times {10}^{- 3} s^{- 1} \right) \right]\]
(b) As per the question
For the wave equation ,we need to find the displacement and velocity at x = 2 cm and t = 0.
\[y = \left( 0 . 2 \right) cm \sin2\pi = 0\]
\[ \therefore \nu = A\omega cos\pi x\]
\[ = 0 . 2 \times 2000\pi \times \cos2\pi\]
\[ = 400\pi\]
\[ = 400\pi cm/s = 4\pi m/s\]
If the wave equation is written in a different fashion, then also we will get the same values for these quantities.
APPEARS IN
RELATED QUESTIONS
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m s–1, (b) recedes from the platform with a speed of 10 m s–1? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 m s–1.
Choose the correct option:
Which of the following equations represents a wave travelling along Y-axis?
Velocity of sound in air is 332 m s−1. Its velocity in vacuum will be
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
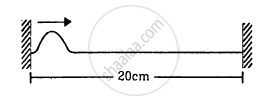
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
A 2⋅00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
A man standing unsymmetrical position between two mountains and fires a gun. He hears the first echo after 1.5 s and the second echo after 2.5 s. If the speed of sound in air is 340 m/s, then the distance between the mountains will be ______
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36t + 0.018x + π/4) where x and y are in cm and t is in s. The positive direction of x is from left to right.
- The wave is travelling from right to left.
- The speed of the wave is 20 m/s.
- Frequency of the wave is 5.7 Hz.
- The least distance between two successive crests in the wave is 2.5 cm.
The amplitude of wave disturbance propagating in the positive x-direction given is by `1/(1 + x)^2` at time t = 0 and `1/(1 + (x - 2)^2)` at t = 1 s, where x and y are in 2 metres. The shape of wave does not change during the propagation. The velocity of the wave will be ______ m/s.
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
