Advertisements
Advertisements
Question
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N m−1 and is stretched by 1⋅0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
Solution
Given,
Length of the string, L = 40 cm
Mass of the string = 10 gm
Mass per unit length
\[= \frac{10}{40} = \frac{1}{4} \left( gm/cm \right)\]
Spring constant, k = 160 N/m
\[Deflection, x = 1 cm\]
\[ = 0 . 01 m\]
\[Tension, T = kx = 160 \times 0 . 01\]
\[ \Rightarrow T = 1 . 6 N = 16 \times {10}^4 dyn\]
\[Now, \]
\[v = \sqrt{\left( \frac{T}{m} \right)} = \sqrt{\left( \frac{16 \times {10}^4}{\frac{1}{4}} \right)}\]
\[ \Rightarrow v = 8 \times {10}^2 cm/s = 800 \text{ cm}/s\]
∴ Time taken by the pulse to reach the spring,
\[t = \frac{40}{800} = \frac{1}{20} = 0 . 05 s\]
APPEARS IN
RELATED QUESTIONS
You have learnt that a travelling wave in one dimension is represented by a function y= f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
(a) `(x – vt )^2`
(b) `log [(x + vt)/x_0]`
(c) `1/(x + vt)`
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1? The operating frequency of the scanner is 4.2 MHz.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of S wave is about 4.0 km s–1, and that of P wave is 8.0 km s–1. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in straight line, at what distance does the earthquake occur?
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
A wave travels along the positive x-direction with a speed of 20 m s−1. The amplitude of the wave is 0⋅20 cm and the wavelength 2⋅0 cm. (a) Write the suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x= 2⋅0 cm at time t = 0 according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?
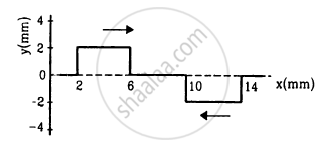
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
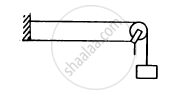
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
A man standing unsymmetrical position between two mountains and fires a gun. He hears the first echo after 1.5 s and the second echo after 2.5 s. If the speed of sound in air is 340 m/s, then the distance between the mountains will be ______
What is the interference of sound waves?
A steel wire has a length of 12 m and a mass of 2.10 kg. What will be the speed of a transverse wave on this wire when a tension of 2.06 × 104N is applied?
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
The displacement y of a particle in a medium can be expressed as, y = `10^-6sin(100t + 20x + pi/4)` m where t is in second and x in meter. The speed of the wave is ______.
