Advertisements
Advertisements
Question
Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of S wave is about 4.0 km s–1, and that of P wave is 8.0 km s–1. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in straight line, at what distance does the earthquake occur?
Solution 1
Let vSand vP be the velocities of S and P waves respectively.
Let L be the distance between the epicentre and the seismograph.
We have:
L = vStS (i)
L = vPtP (ii)
Where,
tS and tP are the respective times taken by the S and P waves to reach the seismograph from the epicentre
It is given that:
vP = 8 km/s
vS = 4 km/s
From equations (i) and (ii), we have:
vS tS = vP tP
4tS = 8 tP
tS = 2 tP (iii)
It is also given that:
tS – tP = 4 min = 240 s
2tP – tP = 240
tP = 240
And tS = 2 × 240 = 480 s
From equation (ii), we get:
L = 8 × 240
= 1920 km
Hence, the earthquake occurs at a distance of 1920 km from the seismograph
Solution 2
Here speed of S wave, υs = 4.0 km s-1 and speed of P wave, υp = 8.0 km s-1. Time gap between P and S waves reaching the resimograph, t = 40 min = 240 s.
Let distance of earthquake centre = sKm
`:. t = t_s - t_p = S/v_s - S/v_p = S/4.0 - S/8.0 = S/8.0 = 240 s`
or `s = 240 xx 8.0 = 1920 km`
APPEARS IN
RELATED QUESTIONS
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m s–1, (b) recedes from the platform with a speed of 10 m s–1? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 m s–1.
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
A sine wave is travelling in a medium. A particular particle has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave? (b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4 cm \right) \sin\left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
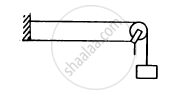
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
