Advertisements
Advertisements
Question
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
Solution 1
Here, h = 300 m, g = 9.8 ms-2 and velocity of sound, v = 340 ms-1 Let t1be the time taken by the stone to reach at the surface of pond.
Then using `s = ut + 1/2 at^2 1/2 at^2 => h = 0 xx t + 1/2 "gt"_1^2`
`:. t_1 = sqrt((2xx300)/9.8) = 7.82 s`
Also if `t_2` is the time taken by the sound to reach at a height h, then
`t_2 = h/v = 300/340 = 0.88 s`
:. Total time after which sound of splash is heard = `t_1 + t_2`
= 7.82 + 0.88 = 8.7 s
Solution 2
Height of the tower, s = 300 m
Initial velocity of the stone, u = 0
Acceleration, a = g = 9.8 m/s2
Speed of sound in air = 340 m/s
The time (`t_1`) taken by the stone to strike the water in the pond can be calculated using the second equation of motion, as:
`s= ut_1 + 1/2 "gt"_1^2`
`300 = 0 + 1/2 xx 9.8 xx t_1^2`
`:. t_1 =sqrt((300xx2)/9.8) = 7.82 s`
Time taken by the sound to reach the top of the tower, `t_2 = 300/340 = 0.88 s`
Therefore, the time after which the splash is heard,`t = t_1 + t_2`
= 7.82 + 0.88 = 8.7 s
APPEARS IN
RELATED QUESTIONS
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
A train, standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is the frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m s–1, (b) recedes from the platform with a speed of 10 m s–1? (ii) What is the speed of sound in each case? The speed of sound in still air can be taken as 340 m s–1.
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will ______.
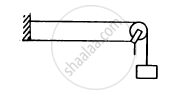
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
Speed of sound wave in air ______.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
Given below are some functions of x and t to represent the displacement of an elastic wave.
- y = 5 cos (4x) sin (20t)
- y = 4 sin (5x – t/2) + 3 cos (5x – t/2)
- y = 10 cos [(252 – 250) πt] cos [(252 + 250)πt]
- y = 100 cos (100πt + 0.5x)
State which of these represent
- a travelling wave along –x direction
- a stationary wave
- beats
- a travelling wave along +x direction.
Given reasons for your answers.
