Advertisements
Advertisements
Question
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
Solution
Given,
Equation of the wave travelling on a string stretched along the X-axis:
\[y = Ae {}^\left( \frac{x}{a} + \frac{t}{T} \right) {{}^-}^2 \]
(a) The dimensions of A (amplitude), T (time period) and \[a = \frac{\lambda}{2\pi}\] , which will have the dimensions of the wavelength, are as follows:
\[\left[ A \right] = \left[ M^0 L^1 T^0 \right]\]
\[\left[ T \right] = \left[ M^0 L^0 T^{- 1} \right]\]
\[\left[ a \right] = \left[ M^0 L^1 T^0 \right]\]
(b) Wave speed, \[\nu = \frac{\lambda}{T} = \frac{a}{T} \left[ \lambda = a \right]\]
(c) If \[y = f \left( t + \frac{x}{\nu} \right)\] , then the wave travels in the negative direction; and if \[y = f \left( t - \frac{x}{\nu} \right)\] ,then the wave travels in the positive direction.
Thus, we have:
`"y"="Ae"^[[(x/a)+(t/T)]^(-2)]`
\[ = A e^{- \frac{1}{T} \left[ t + \left( \frac{xT}{a} \right) \right]^2} \]
\[ = A e^{- \frac{1}{T}\left[ t + \frac{x}{V} \right]} \]
\[ = A e^{- f\left[ t + \frac{x}{V} \right]}\]
Hence, the wave is travelling is the negative direction.
(d) Wave speed, \[v = \frac{a}{t}\] Maximum pulse at t = T = \[\left( \frac{a}{T} \right) \times T = a\] (Along the negative x - axis)
Maximum pulse at t = 2T = \[\left( \frac{a}{T} \times 2T \right) = 2a \] (Along the negative x - axis)
Therefore, the wave is travelling in the negative x-direction.
APPEARS IN
RELATED QUESTIONS
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1? The operating frequency of the scanner is 4.2 MHz.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
Velocity of sound in air is 332 m s−1. Its velocity in vacuum will be
Two wires A and B, having identical geometrical construction, are stretched from their natural length by small but equal amount. The Young modules of the wires are YA and YB whereas the densities are \[\rho_A \text{ and } \rho_B\]. It is given that YA > YB and \[\rho_A > \rho_B\]. A transverse signal started at one end takes a time t1 to reach the other end for A and t2 for B.
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
A sonometer wire supports a 4 kg load and vibrates in fundamental mode with a tuning fork of frequency 416. Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave? (b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
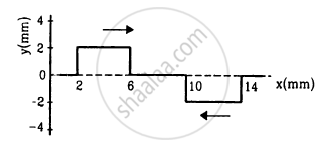
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `λ/2`.
A string of mass 2.5 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in ______.
Speed of sound waves in a fluid depends upon ______.
- directty on density of the medium.
- square of Bulk modulus of the medium.
- inversly on the square root of density.
- directly on the square root of bulk modulus of the medium.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
