Advertisements
Advertisements
प्रश्न
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
उत्तर
Given,
Equation of the wave travelling on a string stretched along the X-axis:
\[y = Ae {}^\left( \frac{x}{a} + \frac{t}{T} \right) {{}^-}^2 \]
(a) The dimensions of A (amplitude), T (time period) and \[a = \frac{\lambda}{2\pi}\] , which will have the dimensions of the wavelength, are as follows:
\[\left[ A \right] = \left[ M^0 L^1 T^0 \right]\]
\[\left[ T \right] = \left[ M^0 L^0 T^{- 1} \right]\]
\[\left[ a \right] = \left[ M^0 L^1 T^0 \right]\]
(b) Wave speed, \[\nu = \frac{\lambda}{T} = \frac{a}{T} \left[ \lambda = a \right]\]
(c) If \[y = f \left( t + \frac{x}{\nu} \right)\] , then the wave travels in the negative direction; and if \[y = f \left( t - \frac{x}{\nu} \right)\] ,then the wave travels in the positive direction.
Thus, we have:
`"y"="Ae"^[[(x/a)+(t/T)]^(-2)]`
\[ = A e^{- \frac{1}{T} \left[ t + \left( \frac{xT}{a} \right) \right]^2} \]
\[ = A e^{- \frac{1}{T}\left[ t + \frac{x}{V} \right]} \]
\[ = A e^{- f\left[ t + \frac{x}{V} \right]}\]
Hence, the wave is travelling is the negative direction.
(d) Wave speed, \[v = \frac{a}{t}\] Maximum pulse at t = T = \[\left( \frac{a}{T} \right) \times T = a\] (Along the negative x - axis)
Maximum pulse at t = 2T = \[\left( \frac{a}{T} \times 2T \right) = 2a \] (Along the negative x - axis)
Therefore, the wave is travelling in the negative x-direction.
APPEARS IN
संबंधित प्रश्न
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
You have learnt that a travelling wave in one dimension is represented by a function y= f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
(a) `(x – vt )^2`
(b) `log [(x + vt)/x_0]`
(c) `1/(x + vt)`
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the transmitted sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
The radio and TV programmes, telecast at the studio, reach our antenna by wave motion. Is it a mechanical wave or nonmechanical?
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will ______.
A wave travels along the positive x-direction with a speed of 20 m s−1. The amplitude of the wave is 0⋅20 cm and the wavelength 2⋅0 cm. (a) Write the suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x= 2⋅0 cm at time t = 0 according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?
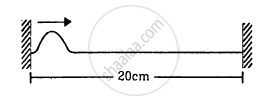
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g m−1 kept under a tension of 60 N. (a) Find the average power transmitted across a given point on the string. (b) Find the total energy associated with the wave in a 2⋅0 m long portion of the string.
A wire of length 2⋅00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
A steel wire fixed at both ends has a fundamental frequency of 200 Hz. A person can hear sound of maximum frequency 14 kHz. What is the highest harmonic that can be played on this string which is audible to the person?
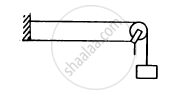
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
What is the interference of sound waves?
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `λ/2`.
