Advertisements
Advertisements
प्रश्न
Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of S wave is about 4.0 km s–1, and that of P wave is 8.0 km s–1. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in straight line, at what distance does the earthquake occur?
उत्तर १
Let vSand vP be the velocities of S and P waves respectively.
Let L be the distance between the epicentre and the seismograph.
We have:
L = vStS (i)
L = vPtP (ii)
Where,
tS and tP are the respective times taken by the S and P waves to reach the seismograph from the epicentre
It is given that:
vP = 8 km/s
vS = 4 km/s
From equations (i) and (ii), we have:
vS tS = vP tP
4tS = 8 tP
tS = 2 tP (iii)
It is also given that:
tS – tP = 4 min = 240 s
2tP – tP = 240
tP = 240
And tS = 2 × 240 = 480 s
From equation (ii), we get:
L = 8 × 240
= 1920 km
Hence, the earthquake occurs at a distance of 1920 km from the seismograph
उत्तर २
Here speed of S wave, υs = 4.0 km s-1 and speed of P wave, υp = 8.0 km s-1. Time gap between P and S waves reaching the resimograph, t = 40 min = 240 s.
Let distance of earthquake centre = sKm
`:. t = t_s - t_p = S/v_s - S/v_p = S/4.0 - S/8.0 = S/8.0 = 240 s`
or `s = 240 xx 8.0 = 1920 km`
APPEARS IN
संबंधित प्रश्न
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
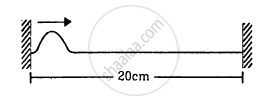
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
What is the interference of sound waves?
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 0.5 m.
A wave of frequency υ = 1000 Hz, propagates at a velocity v = 700 m/sec along x-axis. Phase difference at a given point x during a time interval M = 0.5 × 10-3 sec is ______.
An engine is approaching a cliff at a constant speed. When it is at a distance of 0.9 km from cliff it sounds a whistle. The echo of the sound is heard by the driver after 5 seconds. Velocity of sound in air is equal to 330 ms-1. The speed of the engine is ______ km/h.
