Question

The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4  cm \right)  \sin\left[ \left( 0 \cdot 314  {cm}^{- 1} \right)  x \right]  \cos  \left[ \left( 600\pi  s^{- 1} \right)  t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?

Answer 1

Given:he stationary wave equation of a string vibrating in its third harmonic is given by
y = (0.4 cm) sin [(0.314 cm⁻¹) x]cos [(.600 πs⁻¹) t]
By comparing with standard equation,
\[y = A \sin (kx) \cos (wt)\]
(a) From the above equation, we can infer the following:
\[\omega = 600  \pi\]
\[\Rightarrow 2\pi f = 600 \pi\]
\[ \Rightarrow f = 300 Hz\]
Wavelength, \[\lambda = \frac{2\pi}{0 . 314} = \frac{\left( 2 \times 3 . 14 \right)}{0 . 314}\]
\[\Rightarrow \lambda = 20 \text{ cm }\]
(b) Therefore, the nodes are located at 0cm, 10 cm, 20 cm, 30 cm.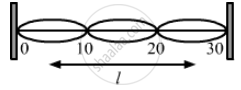

(c) Length of the string, l = \[n\frac{\lambda}{2}\]
\[\Rightarrow l = \frac{3\lambda}{2} = \frac{3 \times 20}{2} = 30  \text{ cm }\]

(d) \[y = 0 . 4  \sin  \left( 0 . 314  x \right)  \cos  \left( 600  \pi t \right)\] 
\[= 0 . 4\sin\left\{ \left( \frac{\pi}{10} \right)  x \right\}\cos\left( 600\pi t \right)\]
\[\lambda\] and \[\nu\] are the wavelength and velocity of the waves that interfere to give this vibration. 

\[\lambda = 20  cm\] 

\[\nu = \frac{\omega}{k} = \frac{600  \pi}{\left( \frac{\pi}{10} \right)} = 6000  \text{ cm/s }\] 

\[ \Rightarrow \nu = 60  \text{ m/s }\]