Advertisements
Advertisements
Question
A steel wire has a length of 12 m and a mass of 2.10 kg. What will be the speed of a transverse wave on this wire when a tension of 2.06 × 104N is applied?
Advertisements
Solution
Given, the length of the wire l = 12 m
Mass of wire m = 2.10 kg
Tension T = 2.06 × 104N
Speed of transverse wave v = `sqrt(T/μ)` .....[Where μ = mass per unit length]
= `sqrt((2.06 xx 10^4)/(((2.10)/12)`
= `sqrt((2.06 xx 12 xx 10^4)/2.10`
= 343 m/s
APPEARS IN
RELATED QUESTIONS
A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
Earthquakes generate sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of S wave is about 4.0 km s–1, and that of P wave is 8.0 km s–1. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in straight line, at what distance does the earthquake occur?
Choose the correct option:
Which of the following equations represents a wave travelling along Y-axis?
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
Two wires A and B, having identical geometrical construction, are stretched from their natural length by small but equal amount. The Young modules of the wires are YA and YB whereas the densities are \[\rho_A \text{ and } \rho_B\]. It is given that YA > YB and \[\rho_A > \rho_B\]. A transverse signal started at one end takes a time t1 to reach the other end for A and t2 for B.
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
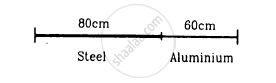
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4 cm \right) \sin\left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
A 2⋅00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m.
Given below are some functions of x and t to represent the displacement of an elastic wave.
- y = 5 cos (4x) sin (20t)
- y = 4 sin (5x – t/2) + 3 cos (5x – t/2)
- y = 10 cos [(252 – 250) πt] cos [(252 + 250)πt]
- y = 100 cos (100πt + 0.5x)
State which of these represent
- a travelling wave along –x direction
- a stationary wave
- beats
- a travelling wave along +x direction.
Given reasons for your answers.
