Advertisements
Advertisements
प्रश्न
A 2⋅00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
उत्तर
Given:
Length of the long rope (L) = 2.00 m
Mass of the rope = 80 g = 0.08 kg
Tension (T) = 256 N
Linear mass density, m
\[= \frac{0 . 08}{2} = 0 . 04 \text{ kg/m }\]
\[Tension, T = 256 N\]
\[Wave velocity, v = \sqrt{\frac{T}{m}}\]
\[ \Rightarrow v = \sqrt{\left( \frac{256}{0 . 04} \right)} = \frac{160}{2}\]
\[ \Rightarrow v = 80 \text{ m/s }\]
For fundamental frequency:
\[L = \frac{\lambda}{4}\]
\[ \Rightarrow \lambda = 4L = 4 \times 2 = 8 m\]
\[ \Rightarrow f = \frac{v}{\lambda} = \frac{80}{8} = 10 \text{ Hz }\]
(a) The frequency overtones are given below:
\[\text{ 1st overtone } = 3f = 30 \text{ Hz }\]
\[\text{ 2nd overtone } = 5f = 50 \text{ Hz }\]
(b) \[\lambda = 4l = 4 \times 2 = 8 m\]
\[\therefore \lambda_1 = \frac{v}{f_1} = \frac{80}{30} = 2 . 67 m\]
\[ \lambda_2 = \frac{v}{f_2} = \frac{80}{50} = 1 . 6 m\]
Hence, the wavelengths are 8 m, 2.67 m and 1.6 m, respectively.
APPEARS IN
संबंधित प्रश्न
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
The radio and TV programmes, telecast at the studio, reach our antenna by wave motion. Is it a mechanical wave or nonmechanical?
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
A sine wave is travelling in a medium. A particular particle has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
Velocity of sound in air is 332 m s−1. Its velocity in vacuum will be
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
A wire of length 2⋅00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
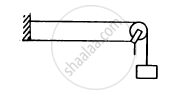
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
A wave of frequency υ = 1000 Hz, propagates at a velocity v = 700 m/sec along x-axis. Phase difference at a given point x during a time interval M = 0.5 × 10-3 sec is ______.
An engine is approaching a cliff at a constant speed. When it is at a distance of 0.9 km from cliff it sounds a whistle. The echo of the sound is heard by the driver after 5 seconds. Velocity of sound in air is equal to 330 ms-1. The speed of the engine is ______ km/h.
The displacement y of a particle in a medium can be expressed as, y = `10^-6sin(100t + 20x + pi/4)` m where t is in second and x in meter. The speed of the wave is ______.
