Advertisements
Advertisements
Question
A transverse harmonic wave on a string is described by y(x, t) = 3.0 sin (36 t + 0.018 x + π/4)
Where x and y are in cm and t in s. The positive direction of x is from left to right.
(a) Is this a travelling wave or a stationary wave?
If it is travelling, what are the speed and direction of its propagation?
(b) What are its amplitude and frequency?
(c) What is the initial phase at the origin?
(d) What is the least distance between two successive crests in the wave?
Advertisements
Solution 1
(a) Yes; Speed = 20 m/s, Direction = Right to left
(b) 3 cm; 5.73 Hz
(c) `pi/4`
(d) 3.49 m
Explanation:
(a) The equation of a progressive wave travelling from right to left is given by the displacement function:
y (x, t) = a sin (ωt + kx + Φ) … (i)
The given equation is:
`y(x,t) = 3.0 sin (36t + 0.018 x + pi/4)` ...(ii)
On comparing both the equations, we find that equation (ii) represents a travelling wave, propagating from right to left.
Now, using equations (i) and (ii), we can write:
ω = 36 rad/s and k = 0.018 m–1
We know that:
`v = omega/(2pi)` and `lambda = (2pi)/k`
Also
= νλ
`:. v = (omega/2pi) xx ((2pi)/k) = omega/k`
`= 36/0.018 = 2000 "cm/s" = 20 "m/s"`
Hence, the speed of the given travelling wave is 20 m/s.
b) Amplitude of the given wave, a = 3 cm
Frequency of the given wave:
`v =omega/(2pi) = 36/(2xx3.14)= 5.73 "Hz"`
(c) On comparing equations (i) and (ii), we find that the initial phase angle, `phi = pi/4`
(d) The distance between two successive crests or troughs is equal to the wavelength of the wave.
Wavelength is given by the relation: k = `(2pi)/lambda`
`:. lambda = (2pi)/k = (2xx3.14)/(0.018) = 348.89 cm = 3.49 m`
Solution 2
The given equation is y(x,t) = `3.0 sin (36t + 0.018x + pi/4)` , where x and y are in cm and t in s.
a) The equation is the equation of a travelling wave, travelling from right to left (i.e along -ve direction of x because it is an equation of the type )
`y(x,t) = A sin(omegat + kx + phi)`
Here A = 3.0 cm, `omega = 36 "rad s"^(-1)`, k = 0.018 cm and `phi = pi/4`
:. Speed of wave propagation,
`v = omega/k = (36 " rad s"^(-1))/(0.018 cm^(-1)) = (36 "rad s"^(-1))/(0.018 xx 10^2 "ms^(-1)) = 20 ms^(-1)`
b) Amplitude of wave, A = 3.0 cm = 0.03 m
Frequency of wave `v = omega/(2pi) = 36/(2pi) = 5.7` Hz
c) Initial phase at the origin, `phi = pi/4`
d) Least distance between two successive crests in the wave
`= lambda = (2pi)/k = (2pi)/0.018`
= 349 cm = 3.5 m
RELATED QUESTIONS
When longitudinal wave is incident at the boundary of denser medium, then............................
- compression reflects as a compression.
- compression reflects as a rarefaction.
- rarefaction reflects as a compression.
- longitudinal wave reflects as transverse wave.
When a transverse wave on a string is reflected from the free end, the phase change produced is ..............
(a) zero rad
(b) ` pi/2 ` rad
(c) `(3pi)/4` rad
(d) `pi` rad
A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
y = cos x sin t + cos 2x sin 2t
A transverse wave is produced on a stretched string 0.9 m long and fixed at its ends. Find the speed of the transverse wave, when the string vibrates while emitting the second overtone of frequency 324 Hz.
A mechanical wave propagates in a medium along the X-axis. The particles of the medium
(a) must move on the X-axis
(b) must move on the Y-axis
(c) may move on the X-axis
(d) may move on the Y-axis.
A wave going in a solid
(a) must be longitudinal
(b) may be longitudinal
(c) must be transverse
(d) may be transverse.
A wave moving in a gas
Mark out the correct options.
A particle on a stretched string supporting a travelling wave, takes 5⋅0 ms to move from its mean position to the extreme position. The distance between two consecutive particles, which are at their mean positions, is 2⋅0 cm. Find the frequency, the wavelength and the wave speed.
A vertical rod is hit at one end. What kind of wave propagates in the rod if (a) the hit is made vertically (b) the hit is made horizontally?
A transverse wave described by \[y = \left( 0 \cdot 02 m \right) \sin \left( 1 \cdot 0 m^{- 1} \right) x + \left( 30 s^{- 1} \right)t\] propagates on a stretched string having a linear mass density of \[1 \cdot 2 \times {10}^{- 4} kg m^{- 1}\] the tension in the string.
Two blocks each having a mass of 3⋅2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB (See following figure). The linear mass density of the wire AB is 10 g m−1 and that of CD is 8 g m−1. Find the speed of a transverse wave pulse produced in AB and CD.
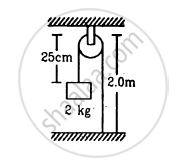
In the arrangement shown in figure , the string has a mass of 4⋅5 g. How much time will it take for a transverse disturbance produced at the floor to reach the pulley? Take g = 10 m s−2.
A heavy but uniform rope of length L is suspended from a ceiling. (a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end. (b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach the ceiling? (c) A particle is dropped from the ceiling at the instant the bottom end is given the jerk. Where will the particle meet the pulse?
If the speed of a transverse wave on a stretched string of length 1 m is 60 m−1, what is the fundamental frequency of vibration?
A steel wire of mass 4⋅0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies? (c) Which overtones are these frequencies? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string?
The equation of a standing wave, produced on a string fixed at both ends, is
\[y = \left( 0 \cdot 4 cm \right) \sin \left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
What could be the smallest length of the string?
The phenomenon of beats can take place
