Advertisements
Advertisements
प्रश्न
A uniform disc of mass 100g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along with a horizontal table with a velocity of 20 cms-1. (take the surface of the table as reference)
उत्तर
Mass of the disc = 100 g = 100 x 10-3 kg = `1/10`kg
Velocity of disc = 20 cm s-1 = 20 x 10-2 ms-1 = 0.2 ms-1
r = 5 cm = `5 xx 10^-2 m, omega = v/r = (20 xx 10^-2)/(5 xx 10^-2) = 4`
Energy = `1/2mV^2 + 1/2Iomega^2 = 1/2(mV^2 + Iomega^2),` where I = `1/2mr^2`
= `1/2[1/10 xx 0.2 xx 0.2 + 1/2 xx 1/10 xx 25 xx 1/10^4 xx 16]`
= `1/2[4/1000 + 2/1000] = 1/2[6/1000]`
Energy = `3 xx 10^-3` J
APPEARS IN
संबंधित प्रश्न
Read each statement below carefully, and state, with reasons, if it is true or false;
For perfect rolling motion, work done against friction is zero.
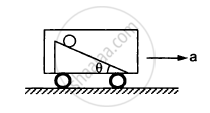
The following figure shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline θ is related to the acceleration a of the car as a = g tanθ. If the sphere is set in pure rolling on the incline, _____________.
A solid sphere of mass 0⋅50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
Answer in Brief:
A rigid object is rolling down an inclined plane derive the expression for the acceleration along the track and the speed after falling through a certain vertical distance.
A disc of the moment of inertia Ia is rotating in a horizontal plane about its symmetry axis with a constant angular speed ω. Another disc initially at rest of moment of inertia Ib is dropped coaxially onto the rotating disc. Then, both the discs rotate with the same constant angular speed. The loss of kinetic energy due to friction in this process is, ______
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with velocity of 10 emfs. The total kinetic energy of sphere is ______.
A man is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre at an angular velocity `omega`. The tension in the strings is F. If the length of string and angular velocity are doubled, the tension in string is now ____________.
A 1000 kg car has four 10 kg wheels. When the car is moving, fraction of total K.E. of the car due to rotation of the wheels about their axles is nearly (Assume wheels be uniform disc)
A solid sphere of mass 2 kg is rolling on a frictionless horizontal surface with velocity 6m/s. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be ______.
(Force constant of the spring = 36 N/m)
The kinetic energy and angular momentum of a body rotating with constant angular velocity are E and L. What does `(2E)/L` represent?
