Advertisements
Advertisements
Question
A uniform disc of mass 100g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along with a horizontal table with a velocity of 20 cms-1. (take the surface of the table as reference)
Solution
Mass of the disc = 100 g = 100 x 10-3 kg = `1/10`kg
Velocity of disc = 20 cm s-1 = 20 x 10-2 ms-1 = 0.2 ms-1
r = 5 cm = `5 xx 10^-2 m, omega = v/r = (20 xx 10^-2)/(5 xx 10^-2) = 4`
Energy = `1/2mV^2 + 1/2Iomega^2 = 1/2(mV^2 + Iomega^2),` where I = `1/2mr^2`
= `1/2[1/10 xx 0.2 xx 0.2 + 1/2 xx 1/10 xx 25 xx 1/10^4 xx 16]`
= `1/2[4/1000 + 2/1000] = 1/2[6/1000]`
Energy = `3 xx 10^-3` J
APPEARS IN
RELATED QUESTIONS
Derive an expression for kinetic energy, when a rigid body is rolling on a horizontal surface without slipping. Hence find kinetic energy for a solid sphere.
A stone of mass 2 kg is whirled in a horizontal circle attached at the end of 1.5m long string. If the string makes an angle of 30° with vertical, compute its period. (g = 9.8 m/s2)
Discuss the interlink between translational, rotational and total kinetic energies of a rigid object rolls without slipping.
A pendulum consisting of a massless string of length 20 cm and a tiny bob of mass 100 g is set up as a conical pendulum. Its bob now performs 75 rpm. Calculate kinetic energy and increase in the gravitational potential energy of the bob. (Use π2 = 10)
What is the condition for pure rolling?
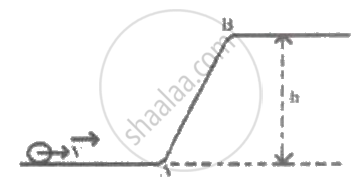
A solid sphere is rolling on a frictionless surface with translational velocity 'V'. It climbs the inclined plane from 'A' to 'B' and then moves away from Bon the smooth horizontal surface. The value of 'V' should be ______.
The angular velocity of minute hand of a clock in degree per second is ______.
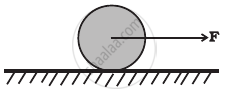
A uniform disc of radius R, is resting on a table on its rim.The coefficient of friction between disc and table is µ (Figure). Now the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping?
A circular disc reaches from top to bottom of an inclined plane of length 'L'. When it slips down the plane, it takes time ' t1'. when it rolls down the plane, it takes time t2. The value of `t_2/t_1` is `sqrt(3/x)`. The value of x will be ______.
A disc of mass 4 kg rolls on a horizontal surface. If its linear speed is 3 m/ s, what is its total kinetic energy?
