Advertisements
Advertisements
प्रश्न
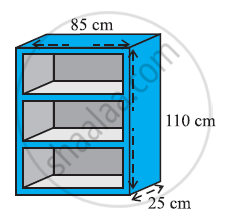
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
उत्तर
External height (l) of book self = 85 cm
External breadth (b) of book self = 25 cm
External height (h) of book self = 110 cm
External surface area of shelf while leaving out the front face of the shelf
= lh + 2 (lb + bh)
= [85 × 110 + 2 (85 × 25 + 25 × 110)] cm2
= (9350 + 9750) cm2
= 19100 cm2
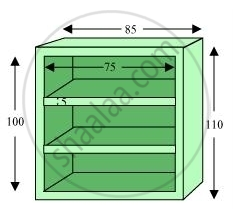
Area of front face = [85 × 110 − 75 × 100 + 2 (75 × 5)] cm2
= 1850 + 750 cm2
= 2600 cm2
Area to be polished = (19100 + 2600) cm2 = 21700 cm2
Cost of polishing 1 cm2 area = Rs 0.20
Cost of polishing 21700 cm2 area Rs (21700 × 0.20) = Rs 4340

It can be observed that length (l), breadth (b), and height (h) of each row of the book shelf is 75 cm, 20 cm, and 30 cm respectively.
Area to be painted in 1 row = 2 (l + h) b + lh
= [2 (75 + 30) × 20 + 75 × 30] cm2
= (4200 + 2250) cm2
= 6450 cm2
Area to be painted in 3 rows = (3 × 6450) cm2 = 19350 cm2
Cost of painting 1 cm2 area = Rs 0.10
Cost of painting 19350 cm2 area = Rs (19350 × 0.1)
= Rs 1935
Total expense required for polishing and painting = Rs (4340 + 1935)
= Rs 6275
Therefore, it will cost Rs 6275 for polishing and painting the surface of the bookshelf.
APPEARS IN
संबंधित प्रश्न
Find the volume of a sphere whose radius is 0.63 m.
`["Assume "pi=22/7]`
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
`["Assume "pi=22/7]`
Find the volume of a sphere whose diameter is 2.1 m .
A hemispherical tank has inner radius of 2.8 m. Find its capacity in litres.
A vessel in the form of a hemispherical bowl is full of water. Its contents are emptied in a right circular cylinder. The internal radii of the bowl and the cylinder are 3.5 cm and 7 cm respectively. Find the height to which the water will rise in the cylinder.
A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder
A hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
A hemispherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 litres per second. How much time will it take to empty the tank completely?
Metal spheres, each of radius 2 cm, are packed into a rectangular box of internal dimensions 16 cm × 8 cm × 8 cm. When 16 spheres are packed the box is filled with preservative liquid. Find the volume of this liquid. Give your answer to the nearest integer. [Use π = 3.14]
Two solid spheres made of the same metal have weights 5920 g and 740 g, respectively. Determine the radius of the larger sphere, if the diameter of the smaller one is 5 cm.
