Advertisements
Advertisements
प्रश्न
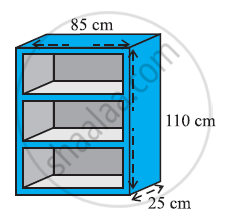
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
उत्तर
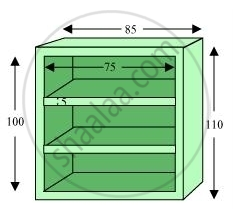
External height (l) of book self = 85 cm
External breadth (b) of book self = 25 cm
External height (h) of book self = 110 cm
External surface area of shelf while leaving out the front face of the shelf
= lh + 2 (lb + bh)
= [85 × 110 + 2 (85 × 25 + 25 × 110)] cm2
= (9350 + 9750) cm2
= 19100 cm2
Area of front face = [85 × 110 − 75 × 100 + 2 (75 × 5)] cm2
= 1850 + 750 cm2
= 2600 cm2
Area to be polished = (19100 + 2600) cm2 = 21700 cm2
Cost of polishing 1 cm2 area = Rs 0.20
Cost of polishing 21700 cm2 area Rs (21700 × 0.20) = Rs 4340

It can be observed that length (l), breadth (b), and height (h) of each row of the book shelf is 75 cm, 20 cm, and 30 cm respectively.
Area to be painted in 1 row = 2 (l + h) b + lh
= [2 (75 + 30) × 20 + 75 × 30] cm2
= (4200 + 2250) cm2
= 6450 cm2
Area to be painted in 3 rows = (3 × 6450) cm2 = 19350 cm2
Cost of painting 1 cm2 area = Rs 0.10
Cost of painting 19350 cm2 area = Rs (19350 × 0.1)
= Rs 1935
Total expense required for polishing and painting = Rs (4340 + 1935)
= Rs 6275
Therefore, it will cost Rs 6275 for polishing and painting the surface of the bookshelf.
APPEARS IN
संबंधित प्रश्न
Find the volume of a sphere whose radius is 0.63 m.
`["Assume "pi=22/7]`
Find the volume of a sphere whose surface area is 154 cm2.
`["Assume "pi=22/7]`
A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of ₹ 4989.60 If the cost of white-washing is ₹ 20 per square meter, find the
- inside surface area of the dome,
- volume of the air inside the dome.
`["Assume "pi=22/7]`
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Find the volume of a sphere whose radius is 3.5 cm.
A shopkeeper has one laddoo of radius 5 cm. With the same material, how many laddoos of radius 2.5 cm can be made?
The diameter of a coper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Find the radius of a sphere if its volume is 904.32 cubic cm. (π = 3.14)
A cube of side 4 cm contains a sphere touching its sides. Find the volume of the gap in between.
