Advertisements
Advertisements
प्रश्न
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base
of the cone is 16 cm and its height is 15 cm. Find the cost of painting the toy at Rs. 7 per 100
`cm^2`.
Advertisements
उत्तर १
Diameter of cone = 16cm.
∴ Radius of cone = 8cm.
Height of cone = 15cm
Slant height of cone - `sqrt(8^2+15^2)`
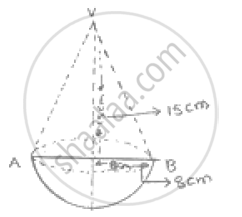
-`sqrt(64+225)`
-`sqrt(289)`
-17 cm
∴ Total curved surface area of toy
-πrl + `2πr^2`
-`22/7 × 8 × 17 + 2 × 22/7 × 8^2`
- `5808/7cm^2`
Now .cost of `100cm^2 - Rs.7`
`1cm^2 - Rs7/100`
Hence , cost of `5808/7 cm^2 - Rs (5808/7×7/100)`
-Rs.58.08.
उत्तर २
Diameter of cone = 16cm.
∴ Radius of cone = 8cm.
Height of cone = 15cm
Slant height of cone - `sqrt(8^2+15^2)`
-`sqrt(64+225)`
-`sqrt(289)`
-17 cm
∴ Total curved surface area of toy
-πrl + `2πr^2`
-`22/7 × 8 × 17 + 2 × 22/7 × 8^2`
- `5808/7cm^2`
Now .cost of `100cm^2 - Rs.7`
`1cm^2 - Rs7/100`
Hence , cost of `5808/7 cm^2 - Rs (5808/7×7/100)`
-Rs.58.08.
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 21 cm.
`["Assume "pi=22/7]`
Find the total surface area of a hemisphere of radius 10 cm. [Use π = 3.14]
Find the radius of a sphere whose surface area is 154 cm2.
`["Assume "pi=22/7]`
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
Find the surface area of a sphere of radius 10.5 cm.
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved
surface area of the shape if the length of the shape be 7 cm.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their :
- radii,
- surface areas.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm.
A hemi-spherical bowl has negligible thickness and the length of its circumference is 198 cm. Find the capacity of the bowl.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is
A solid, consisting of a right circular cone standing on a hemisphere, is placed upright, in a right circular cylinder, full of water and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer to the nearest cubic centimetre.
Find the volume and surface area of a sphere of diameter 21 cm.
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
The cylinder of radius 12 cm have filled the 20 cm with water. One piece of iron drop in the stands of water goes up 6.75 cm. Find the radius of sphere piece.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
