Advertisements
Advertisements
Question
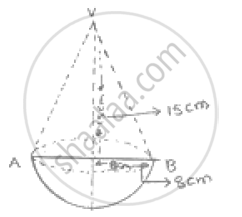
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base
of the cone is 16 cm and its height is 15 cm. Find the cost of painting the toy at Rs. 7 per 100
`cm^2`.
Solution 1
Diameter of cone = 16cm.
∴ Radius of cone = 8cm.
Height of cone = 15cm
Slant height of cone - `sqrt(8^2+15^2)`
-`sqrt(64+225)`
-`sqrt(289)`
-17 cm
∴ Total curved surface area of toy
-πrl + `2πr^2`
-`22/7 × 8 × 17 + 2 × 22/7 × 8^2`
- `5808/7cm^2`
Now .cost of `100cm^2 - Rs.7`
`1cm^2 - Rs7/100`
Hence , cost of `5808/7 cm^2 - Rs (5808/7×7/100)`
-Rs.58.08.
Solution 2
Diameter of cone = 16cm.
∴ Radius of cone = 8cm.
Height of cone = 15cm
Slant height of cone - `sqrt(8^2+15^2)`

-`sqrt(64+225)`
-`sqrt(289)`
-17 cm
∴ Total curved surface area of toy
-πrl + `2πr^2`
-`22/7 × 8 × 17 + 2 × 22/7 × 8^2`
- `5808/7cm^2`
Now .cost of `100cm^2 - Rs.7`
`1cm^2 - Rs7/100`
Hence , cost of `5808/7 cm^2 - Rs (5808/7×7/100)`
-Rs.58.08.
APPEARS IN
RELATED QUESTIONS
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm.
(Use 𝜋 = 3.14)
Assuming the earth to be a sphere of radius 6370 km, how many square kilo metres is area
of the land, if three-fourth of the earth’s surface is covered by water?
The surface area of a solid sphere is increased by 12% without changing its shape. Find the percentage increase in its:
- radius
- volume
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
9 cm
A sphere has the same curved surface area as the curved surface area of a cone of height 36 cm and base radius 15 cm . Find the radius of the sphere .
A solid metallic cylinder has a radius of 2 cm and is 45 cm tall. Find the number of metallic spheres of diameter 6 cm that can be made by recasting this cylinder .
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate : the number of cones recast. `("Take" pi =22/7)`
A sphere cut out from a side of 7 cm cubes. Find the volume of this sphere?
The cylinder of radius 12 cm have filled the 20 cm with water. One piece of iron drop in the stands of water goes up 6.75 cm. Find the radius of sphere piece.
