Advertisements
Advertisements
प्रश्न
आकृती मध्ये जर ∠a ≅ ∠b तर सिद्ध करा रेषा l || रेषा m
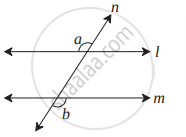
उत्तर
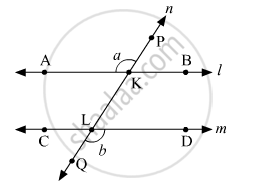
रेषा l वर A आणि B हे बिंदू, रेषा m वर C आणि D हे बिंदू आणि रेषा n वर P आणि Q हे बिंदू चिन्हांकित केले आहेत.
रेषा n ही रेषा l ला K बिंदूत व रेषा m ला L बिंदूत छेदते.
रेषा PQ ही एक सरळ रेषा आहे आणि किरण KA त्यावर उभे आहे, म्हणून.
m∠AKP + m∠AKL = 180∘ ...(रेषीय जोडीतील कोन)
⇒ m∠a + m∠AKL = 180∘
⇒ m∠a = 180∘ − m∠AKL ....(1)
रेषा PQ ही एक सरळ रेषा आहे आणि किरण LD त्यावर उभे आहे म्हणून,
m∠DLQ + m∠DLK = 180∘ ...(रेषीय जोडीतील कोन)
⇒ m∠b + m∠DLK = 180∘
⇒ m∠b = 180∘ − m∠DLK ...(2)
परंतु, ∠a ≅ ∠b, तर m∠a = m∠b
∴ (1) व (2) वरून,
180∘ − m∠AKL = 180∘ − m∠DLK
⇒ m∠AKL = m∠DLK
⇒ ∠AKL ≅ ∠DLK
दोन रेषांना एका छेदिकेने छेदले असता होणाऱ्या व्युत्क्रम काेनांची एक जोडी एकरूप असेल तर त्या रेषा समांतर असतात.
∴ AB || CD किंवा रेषा l || रेषा m.
