Question

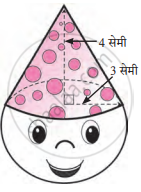
आकृती मध्ये मुलांचे एक खेळणे आहे. ते एक अर्धगोल व एक शंकू यांच्या सहाय्याने केले आहे. आकृतीत दर्शविलेल्या मापांवरून खेळण्याचे घनफळ व पृष्ठफळ काढा. (π = 3.14)

Answer 1

दिलेले: शंकूसाठी,

उंची (h) = 4 सेमी, त्रिज्या (r) = 3 सेमी,

अर्धगोलासाठी,

त्रिज्या (r) = 3 सेमी

शोधा: खेळण्याचे घनफळ व पृष्ठफळ 

उकल:

शंकूची तिरकस उंची (l) = `sqrt(r^2 + h^2)`

= `sqrt(3^2 + 4^2)`

= `sqrt(9 + 16)`

= `sqrt25`

= 5 सेमी

शंकूचे घनफळ = `1/3pir^2h`

= `1/3 xx pi xx 3^2 xx 4`

= 12π सेमी³ 

शंकूचे वक्रपृष्ठफळ = πrl

= π × 3 × 5

= 15π सेमी² 

अर्धगोलाचे घनफळ = `2/3pir^3`

= `2/3 xx pi xx 3^3` = 18π सेमी³ 

अर्धगोलाचे वक्रपृष्ठफळ = 2πr² 

= 2 × π × 3² = 18π सेमी² 

आता, खेळण्याचे घनफळ = शंकूचे घनफळ + अर्धगोलाचे घनफळ

= 12π + 18π

= 30π = 30 × 3.14

= 94.20 सेमी³ 

तसेच, खेळण्याचे पृष्ठफळ = शंकूचे वक्रपृष्ठफळ + अर्धगोलाचे वक्रपृष्ठफळ

= 15π + 18π

= 33π

= 33 × 3.14

= 103.62 सेमी² 

∴ त्या खेळण्याचे घनफळ व पृष्ठफळ अनुक्रमे 94.20 सेमी³ व 103.62 सेमी² आहे.