Advertisements
Advertisements
प्रश्न
आकृति में, ∠BAC = 90° और AD ⊥ BC हैं। तब, ______।
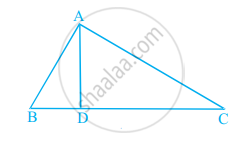
विकल्प
BD . CD = BC2
AB . AC = BC2
BD . CD = AD2
AB . AC = AD2
उत्तर
आकृति में, ∠BAC = 90° और AD ⊥ BC हैं। तब, BD . CD = AD2 ।
स्पष्टीकरण:

∆ADB और ∆ADC से,
प्रश्न के अनुसार, हमारे पास है,
∠D = ∠D = 90° ...(∵ AD ⊥ BC)
∠DBA = ∠DAC ...[प्रत्येक कोण = 90° – ∠C]
AAA समानता मानदंड का उपयोग करते हुए,
∆ADB ∼ ∆ADC
`("BD")/("AD") = ("AD")/("CD")`
BD . CD = AD2
APPEARS IN
संबंधित प्रश्न
निम्नलिखित युग्म के दो भिन्न-भिन्न उदाहरण दीजिए:
समरूप आकृतियाँ
निम्नलिखित युग्म के दो भिन्न-भिन्न उदाहरण दीजिए:
ऐसी आकृतियाँ जो समरूप नहीं हैं।
बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं:

सिद्ध कीजिए कि एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
एक समचतुर्भुज के विकर्णों की लंबाइयाँ 16 cm और 12 cm हैं। तब इस समचतुर्भुज की भुजा की लंबाई ______ है।
