Advertisements
Advertisements
प्रश्न
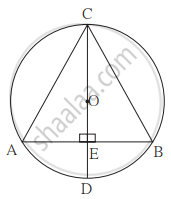
आकृति में O केंद्रवालेवृत्त का व्यास CD तथा जीवा AB है। व्यास CD जीवा AB के बिंदु E पर लंब है तो सिद्ध कीजिए कि ΔABC समद्विबाहु त्रिभुज है।
उत्तर
दत्त: O वृत्त का केंद्र है।
व्यास CD ⊥ जीवा AB, A-E-B
साध्य: ΔABC समद्विबाहु त्रिभुज है।
उपपत्ति:
व्यास CD ⊥ जीवा AB ...(दिया है।)
∴ रेख CD ⊥ जीवा AB ...(C-O-E, O-E-D)
∴ रेख CD ≅ रेख AB ...(वृत्त के केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है) ...(i)
∆CEA तथा ∆CEB में,
∠CEA ≅ ∠CEB ...(प्रत्येक कोण की माप 90°)
रेख AE ≅ रेख BE ...[(i) से]
रेख CE ≅ रेख CE ...(सामान्य भुजा)
∴ ∆CEA ≅ ∆CEB ...(सर्वांगसमता की भु-को-को कसौटी)
∴ रेख AC ≅ रेख BC ...(स.त्रि.सं.भु)
∴ ΔABC समद्विबाहु त्रिभुज है।
APPEARS IN
संबंधित प्रश्न
वृत्त के केंद्र O से 8 सेमी की दूरी पर जीवा AB स्थित है। जीवा AB की लंबाई 12 सेमी है तो वृत्त का व्यास ज्ञात कीजिए।
किसी वृत्त का व्यास 26 सेमी तथा जीवा की लंबाई 24 सेमी है तो वह जीवा वृत्त के केंद्र से कितनी दूरी पर होगी?
34 सेमी त्रिज्यावाले वृत्त की एक जीवा केंद्र से 30 सेमी की दूरी पर हो तो जीवा की लंबाई ज्ञात कीजिए।
O केंद्रवाले वृत्त की त्रिज्या 41 सेमी है। वृत्त की जीवा PQ की लंबाई 80 सेमी हो तो जीवा PQ की केंद्र से दूरी ज्ञात कीजिए।
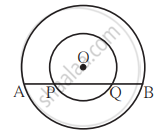
आकृति में बिंदु O केंद्रवाले दो वृत्त हैं। बड़े वृत्त की जीवा AB यह जीवा छोटे वृत्त के बिंदु P तथा Q पर प्रतिच्छेदित करती है। सिद्ध कीजिए कि AP = BQ
सिद्ध कीजिए कि यदि वृत्त का व्यास दो जीवाओं को समद्विभाजित करता हो तो वे जीवाएँ परस्पर समांतर होती हैं।
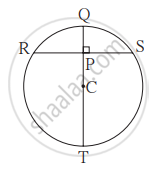
आकृति में C वृत्त का केंद्र है। रेख QT व्यास है। CT = 13, CP = 5 हो तो जीवा RS ज्ञात कीजिए।
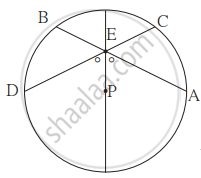
आकृति में P वृत्त का केंद्र है। जीवा AB तथा जीवा CD परस्पर व्यास के बिंदु E पर प्रतिच्छेदित करते हैं। यदि `angle`AEP ≅ `angle`DEP तो सिद्ध कीजिए कि AB = CD