Advertisements
Advertisements
प्रश्न
∆ABC is an equilateral triangle. Point P is on base BC such that PC = `1/3`BC, if AB = 6 cm find AP.
उत्तर

∆ABC is an equilateral triangle.
It is given that,
PC = `1/3`BC
PC = `1/3 xx 6`
PC = 2 cm
∴ BP = BC − PC
= 6 − 2
= 4 cm
Since, ∆ABC is an equilateral triangle, OA is the perpendicular bisector of BC.
OC = `"BC"/2`
= `6/2`
= 3 cm
∴ OP = OC − PC
= 3 − 2
= 1 cm ...(1)
According to Pythagoras theorem,
In ∆AOB,
AB2 = AO2 + OC2
∴ (6)2 = AO2 + (3)2
∴ 36 = AO2 + 9
∴ AO2 = 36 − 9
∴ AO2 = 27
∴ AO = `sqrt27`
∴ AO = `3sqrt3` cm ...(2)
In ∆AOP,
AP2 = AO2 + OP2
∴ AP2 = `(3sqrt3)^2 + (1)^2 `
∴ AP2 = 27 + 1
∴ AP2 = 28
∴ AP = `sqrt28`
∴ AP = `2sqrt7` cm
संबंधित प्रश्न
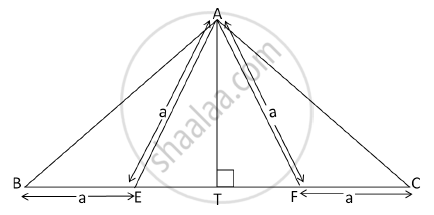
In the following figure, AE = EF = AF = BE = CF = a, AT ⊥ BC. Show that AB = AC = `sqrt3xxa`
Find the length of the side and perimeter of an equilateral triangle whose height is `sqrt3` cm.
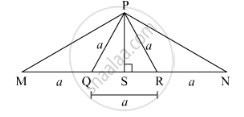
From the information given in the figure, prove that PM = PN = \[\sqrt{3}\] × a
Find the length of the hypotenuse in a right angled triangle where the sum
of the squares of the sides making right angle is 169.
(A)15 (B) 13 (C) 5 (D) 12
Prove that, in a right angled triangle, the square of the hypotenuse is
equal to the sum of the squares of remaining two sides.
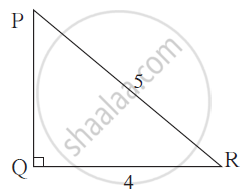
In right angled triangle PQR,
if ∠ Q = 90°, PR = 5,
QR = 4 then find PQ and hence find tan R.
Choose the correct alternative:
ΔABC and ΔDEF are equilateral triangles. If ar(ΔABC): ar(ΔDEF) = 1 : 2 and AB = 4, then what is the length of DE?
From given figure, In ∆ABC, AD ⊥ BC, then prove that AB2 + CD2 = BD2 + AC2 by completing activity.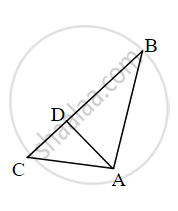
Activity: From given figure, In ∆ACD, By pythagoras theorem
AC2 = AD2 + `square`
∴ AD2 = AC2 – CD2 ......(I)
Also, In ∆ABD, by pythagoras theorem,
AB2 = `square` + BD2
∴ AD2 = AB2 – BD2 ......(II)
∴ `square` − BD2 = AC2 − `square`
∴ AB2 + CD2 = AC2+ BD2
Complete the following activity to find the length of hypotenuse of right angled triangle, if sides of right angle are 9 cm and 12 cm.
Activity: In ∆PQR, m∠PQR = 90°
By Pythagoras Theorem,
PQ2 + `square` = PR2 ......(I)
∴ PR2 = 92 + 122
∴ PR2 = `square` + 144
∴ PR2 = `square`
∴ PR = 15
∴ Length of hypotenuse of triangle PQR is `square` cm.
From given figure, in ∆PQR, if ∠QPR = 90°, PM ⊥ QR, PM = 10, QM = 8, then for finding the value of QR, complete the following activity.

Activity: In ∆PQR, if ∠QPR = 90°, PM ⊥ QR, ......[Given]
In ∆PMQ, by Pythagoras Theorem,
∴ PM2 + `square` = PQ2 ......(I)
∴ PQ2 = 102 + 82
∴ PQ2 = `square` + 64
∴ PQ2 = `square`
∴ PQ = `sqrt(164)`
Here, ∆QPR ~ ∆QMP ~ ∆PMR
∴ ∆QMP ~ ∆PMR
∴ `"PM"/"RM" = "QM"/"PM"`
∴ PM2 = RM × QM
∴ 102 = RM × 8
RM = `100/8 = square`
And,
QR = QM + MR
QR = `square` + `25/2 = 41/2`
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm. Complete the following activity.
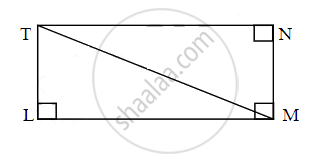
Activity: As shown in figure LMNT is a reactangle.
∴ Area of rectangle = length × breadth
∴ Area of rectangle = `square` × breadth
∴ 192 = `square` × breadth
∴ Breadth = 12 cm
Also,
∠TLM = 90° ......[Each angle of reactangle is right angle]
In ∆TLM,
By Pythagoras theorem
∴ TM2 = TL2 + `square`
∴ TM2 = 122 + `square`
∴ TM2 = 144 + `square`
∴ TM2 = 400
∴ TM = 20
A congruent side of an isosceles right angled triangle is 7 cm, Find its perimeter
ΔPQR, is a right angled triangle with ∠Q = 90°, QR = b, and A(ΔPQR) = a. If QN ⊥ PR, then prove that QN = `(2ab)/sqrt(b^4 + 4a^2)`
