Advertisements
Advertisements
प्रश्न
ΔABC व ΔDEF मध्ये ∠B = ∠E, ∠F = ∠C आणि AB = 3 DE, तर त्या दोन त्रिकोणांबाबत सत्य विधान कोणते?
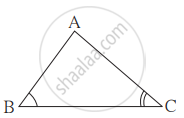
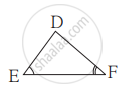
विकल्प
ते एकरूप नाहीत आणि समरूपही नाहीत.
ते समरूप आहेत पण एकरूप नाहीत.
ते एकरूप आहेत आणि समरूपही आहेत.
वरीलपैकी एकही विधान सत्य नाही.
उत्तर
ΔABC व ΔDEF मध्ये ∠B = ∠E, ∠F = ∠C आणि AB = 3 DE, तर त्या दोन त्रिकोणांबाबत सत्य विधान - ते समरूप आहेत पण एकरूप नाहीत, हे आहे.
APPEARS IN
संबंधित प्रश्न
ΔABC ∼ ΔPQR आणि AB : PQ = 2 : 3, तर खालील चौकटी पूर्ण करा.
`("A"(Δ"ABC"))/("A"(Δ"PQR")) = ("AB"^2)/square" = 2^2/3^2 = square/square`
दोन समरूप त्रिकोणांची क्षेत्रफळे 225 चौसेमी व 81 चौसेमी आहेत. जर लहान त्रिकोणाची एक बाजू 12 सेमी असेल तर मोठ्या त्रिकोणाची संगत बाजू काढा.
जर ΔABC ~ ΔPQR आणि AB : PQ = 3:4, तर A(ΔABC) : A(ΔPQR) किती?
जर ΔXYZ ~ ΔPQR आणि A(ΔXYZ) = 25 चौसेमी, A(ΔPQR) = 4 चौसेमी, तर XY : PQ = ?
जर ΔABC ~ ΔDEF आणि ∠A = 45°, ∠E = 35° असल्यास ∠B चे माप किती?
दोन समरूप त्रिकोणांची क्षेत्रफळे 225 चौसेमी, 81 चौसेमी आहेत. जर लहान त्रिकोणाची एक बाजू 12 सेमी असेल, तर मोठ्या त्रिकोणाची संगत बाजू काढा.
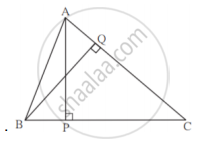
∆ABC मध्ये, AP लंब BC व BQ लंब AC, B-P-C, A-Q-C, तर ∆CPA ~ ∆CQB दाखवा. जर AP = 7, BQ = 8, BC = 12 असल्यास AC ची किंमत काढा.
∆CPA व ∆CQB मध्ये,
∠CPA ≅ `square` ...........[प्रत्येकी 90°]
∠ACP ≅ `square` ...........[सामाईक कोन]
∆CPA ~ ∆CQB ............[`square` समरूपता कसोटी]
`"AP"/"BQ" = square/"BC"` ............…[समरूप त्रिकोणांच्या संगत बाजू प्रमाणात]
`7/8 = square/12`
AC × `square` = 7 × 12
AC = 10.5
दोन समरूप त्रिकोणांपैकी लहान त्रिकोणाच्या बाजू 4 सेमी, 5 सेमी, 6 सेमी लांबीच्या आहेत आणि मोठ्या त्रिकोणाची परिमिती 90 सेमी आहे, तर मोठ्या त्रिकोणाच्या बाजू काढा.
जर ΔABC ∼ ΔPQR, AB : PQ = 4 : 5 आणि A(ΔPQR) = 125 सेमी2 असेल, तर A(ΔABC) काढा.
ΔABC मध्ये रेख DE || बाजू BC. जर 2A(ΔADE) = A(⬜ DBCE), तर AB : AD आणि BC = `sqrt3` DE दाखवा.
