Advertisements
Advertisements
प्रश्न
बिंदु (3, 2) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो रेखा x – 2y = 3 से 45° का कोण बनाती है।
उत्तर
माना रेखा AB का समीकरण: x – 2y = 3
या y = `1/2 "x" - 3`
तब रेखा AB की ढाल = `1/2`
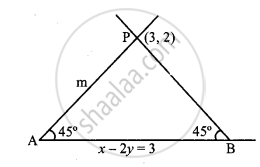
मान लीजिए PA रेखा इसके साथ 45° का कोण बनाती है और इसकी ढाल = m
`± tan 45= ("m" - 1/2)/(1 + "m" xx 1/2)`
या `± 1 = (2"m" - 1)/("m" + 2)`
+ve चिन्ह लेने पर, 1 = `(2"m" - 1)/("m" + 2)`
या 2m – 1 = m + 2
∴ m = 3
2m –1
– ve चिन्ह लेने पर, –1 = `(2"m" - 1)/("m" + 2)`
या 2m – 1 = –m – 2
∴ 3m = –1
या m = `(-1)/3`
अतः रेखा PA का समीकरण जहाँ बिंदु P = (3, 2) हो और m = `(-1)/3` हो।
y – 2 = `- (-1)/3 ("x" - 3)`
3y – 6 = – x + 3
या x + 3y – 9 = 0
अब जब ढाल m = 3 हो, तब बिंदु P(3, 2) से रेखा का समीकरण,
y – 2 = 3(x – 3)
y – 2 = 3x – 9
या 3x – y – 7 = 0
APPEARS IN
संबंधित प्रश्न
रेखा की ढाल ज्ञात कीजिए जो मूल बिंदु और P(0, −4) तथा B(8, 0) बिंदुओं को मिलाने वाले रेखाखंड के मध्य बिंदु से जाती है।
पाइथागोरस प्रमेय के प्रयोग बिना दिखलाइए कि बिंदु (4, 4), (3, 5) और (–1, –1) एक समकोण त्रिभुज के शीर्ष हैं।
उस रेखा का समीकरण ज्ञात कीजिए जो y-अक्ष की धन दिशा से वामावर्त्त मापा गया 30° का कोण बनाती है।
x का वह मान ज्ञात कीजिए जिसके लिए बिंदु (x, −1), (2, 1) और (4, 5) संरेख हैं।
दूरी सूत्र का प्रयोग किए बिना दिखलाइए कि बिंदु (−2, −1), (4, 0), (3, 3) और (−3, 2) एक समांतर चतुर्भुज के शीर्ष हैं।
x-अक्ष और (3, – 1) और (4, – 2) बिंदुओं को मिलाने वाली रेखा के बीच का कोण ज्ञात कीजिए।
एक रेखा की ढाल दूसरी रेखा की ढाल का दुगुना है। यदि दोनों के बीच के कोण की स्पर्शज्या (tangent) `1/3` है तो रेखाओं की ढाल ज्ञात कीजिए।
एक रेखा (x1, y1) और (h, k) से जाती है। यदि रेखा की ढाल m है तो दिखाइए k – y1 = m(h – x1).
यदि तीन बिंदु (h, 0), (a, b) और (0, k) एक रेखा पर हैं तो दिखाइए कि `"a"/"h" + "b"/"k" = 1`
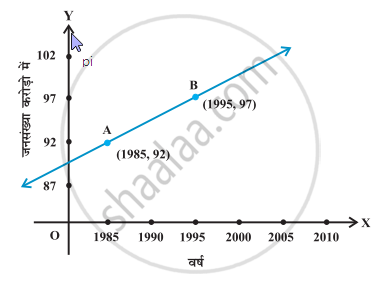
जनसंख्या और वर्ष के निम्नलिखित लेखाचित्र पर विचार कीजिए। रेखा AB की ढाल ज्ञात कीजिए और इसके प्रयोग से बताइए कि वर्ष 2010 में जनसंख्या कितनी होगी?
k के मान । ज्ञात कीजिए जबकि रेखा (k – 3)x – (4 – k2)y + k2 – 7k + 6 = 0
- x-अक्ष के समांतर है।
- y-अक्ष के समांतर है।
- मूल बिंदु से जाती है।
रेखा `"x"/4 + "y"/6 = 1` पर लंब उस बिंदु से खींची गई रेखा का समीकरण ज्ञात कीजिए जहाँ यह रेखा y-अक्ष से मिलती है।
p का मान ज्ञात कीजिए जिससे तीन रेखाएँ 3x + y – 2 = 0, px + 2y – 3 = 0 और 2x – y – 3 = 0 एक बिंदु पर प्रतिच्छेद करें।
