Advertisements
Advertisements
प्रश्न
बिंदु P(2, 3) की x-अक्ष से दूरी ______ है।
विकल्प
2
3
1
5
उत्तर
बिंदु P (2, 3) की x-अक्ष से दूरी 3 है।
स्पष्टीकरण:
हम जानते हैं कि,
(x, y) पहले चतुर्थांश में कार्टेशियन विमान पर एक बिंदु है।
फिर,
x = Y-अक्ष से लंबवत दूरी और
y = X-अक्ष से लंबवत दूरी
इसलिए, x-अक्ष से लंबवत दूरी = y समन्वय = 3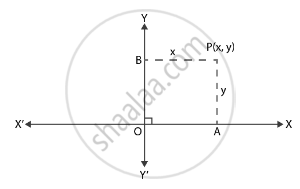
APPEARS IN
संबंधित प्रश्न
(सड़क योजना): एक नगर में दो मुख्य सड़कें हैं, जो नगर के केन्द्र पर मिलती हैं। ये दो सड़कें उत्तर-दक्षिण की दिशा और पूर्व-पश्चिम की दिशा में हैं। नगर की अन्य सभी सड़कें इन मुख्य सड़कों के समांतर परस्पर 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में लगभग पाँच सड़कें हैं। 1 सेंटीमीटर = 200 मीटर का पैमाना लेकर अपनी नोट बुक में नगर का एक मॉडल बनाइए। सड़कों को एकल रेखाओं से निरूपित कीजिए।
आपके मॉडल में एक-दूसरे को काटती हुई अनेक क्रॉस-स्ट्रीट (चौराहे) हो सकती हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, जिनमें से एक उत्तर-दक्षिण दिशा में जाती है और दूसरी पूर्व-पश्चिम की दिशा में। प्रत्येक क्रॉस-स्ट्रीट का निर्देशन इस प्रकार किया जाता है: यदि दूसरी सड़क उत्तर-दक्षिण दिशा में जाती है और पाँचवीं सड़क पूर्व-पश्चिम दिशा में जाती है और ये एक क्रॉसिंग पर मिलती हैं, तब इसे हम क्रॉस-स्ट्रीट (2, 5) कहेंगे। इसी परंपरा से यह ज्ञात कीजिए कि
- कितनी क्रॉस-स्ट्रीटों को (4, 3) माना जा सकता है।
- कितनी क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है।
यदि बिंदुओं (4, p) और (1, 0) के बीच की दूरी 5 है, तो p का मान ______ है।
बिंदु P(– 4, 2), बिंदुओं A(– 4, 6) और B(– 4, – 6) को मिलाने वाले रेखाखंड पर स्थित हैं।
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। ΔABC के केंद्रक के क्या निर्देशांक हैं?
वह बिंदु, जहाँ दोनों निर्देशांक अक्ष मिलते हैं, कहलाता है :
यदि दो बिंदुओं P और Q के निर्देशांक क्रमश : (–2, 3) और (–3, 5) हैं तो (P का भुज) – (Q का भुज) बराबर है :
वह बिंदु जो y-अक्ष की ऋणात्मक दिशा में y-अक्ष पर 5 मात्रक की दूरी पर स्थित है, होगा :
उस बिंदु के निर्देशांक (2, 0) हैं जो y-अक्ष पर x-अक्ष से 2 मात्रक की दूरी पर स्थित है।
उस बिंदु के निर्देशांक ज्ञात कीजिए, जो जिसकी कोटि – 4 है और जो y-अक्ष पर स्थित है।
P(-1, 1), Q(3, -4), R(1, -1), S(-2, -3), T(-4, 4) में से चतुर्थ चतुर्थांश के बिंदु कौन-से हैं?
