Advertisements
Advertisements
प्रश्न
बराबर त्रिज्या 7 cm त्रिज्या वाले चार वृत्ताकार गत्ते के टुकड़ों को एक कागज पर इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को स्पर्श करता है। इन टुकड़ों के बीच में परिबद्ध भाग का क्षेत्रफल ज्ञात कीजिए।
उत्तर
प्रश्न के अनुसार,
चारों वृत्तों को इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को छूता है।
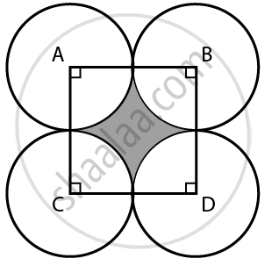
वृत्तों के केन्द्रों को एक रेखाखंड से जोड़ने पर, हमें भुजाओं वाला एक वर्ग ABCD प्राप्त होता है,
AB = BD = DC = CA = 2 ...(त्रिज्या)
= 2(7) cm
= 14 cm
अब, वर्ग का क्षेत्रफल = (भुजा)2
= (14)2
= 196 cm2
ABCD एक वर्ग है,
इसलिए, प्रत्येक कोण का माप 90° होता है।
अर्थात्, ∠A = ∠B = ∠D = ∠C = 90° = `pi/2` त्रिज्या = θ ...(कहें)
मान लें कि,
प्रत्येक त्रिज्यखंड की त्रिज्या = 7 cm
केंद्रीय कोण A के साथ क्षेत्र का क्षेत्रफल A = `(1/2)"r"^2θ`
= `1/2"r"^2θ`
= `1/2 xx 49 xx pi/2`
= `1/2 xx 49 xx 22/(2 xx 7)`
= `77/2 "cm"^2`
चूँकि केंद्रीय कोण और प्रत्येक त्रिज्यखंड की त्रिज्या समान हैं, प्रत्येक त्रिज्यखंड का क्षेत्रफल `77/2 "cm"^2` है।
∴ छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल – चारों त्रिज्यखंडों का क्षेत्रफल
= `196 - (4 xx 77/2)`
= 196 – 154
= 42 cm2
इसलिए, इन टुकड़ों के बीच घिरे हिस्से का अभीष्ट क्षेत्रफल 42 cm2 है।
APPEARS IN
संबंधित प्रश्न
6 सेमी त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60 डिग्री है। `[pi = 22/7 "का प्रयोग करें"]`
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
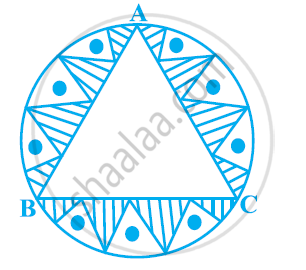
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु ABC त्रिभुज छोड़ते हुए एक डिजाइनर बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
आकृति में, व्यास d वाले एक वृत्त के अंतर्गत एक वर्ग खींचा गया है तथा एक अन्य वर्ग इसी वृत्त के परिगत है। क्या बाहरी वर्ग का क्षेत्रफल आंतरिक वर्ग के क्षेत्रफल का चार गुना है? अपने उत्तर का कारण दीजिए।

s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
एक 20 cm लंबे तार के टुकड़े को मोड़कर एक वृत्त का चाप बनाया गया है, जो इस वृत्त के केंद्र पर 60° का कोण अंतरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
बराबर त्रिज्या 3.5 cm वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
किसी वृत्त के 200° केंद्रीय कोण वाले एक त्रिज्यखंड का क्षेत्रफल 770 cm2 है। इस त्रिज्यखंड के संगत चाप की लंबाई ज्ञात कीजिए।
आकृति में, दिये छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।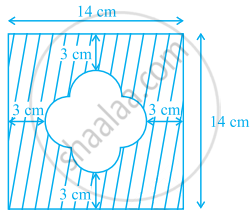
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत दीर्घ त्रिज्यखंड [प्रयोग कीजिए = 3.14]
