Advertisements
Advertisements
प्रश्न
बराबर त्रिज्या 3.5 cm वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
उत्तर
दिया गया है, तीन वृत्त इस प्रकार हैं कि उनमें से प्रत्येक अन्य दो को स्पर्श करता है।
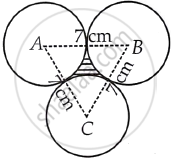
अब, AB, BC और CA को मिलाएँ।
चूँकि, प्रत्येक वृत्त की त्रिज्या 3.5 cm है।
तो, AB = 2 × वृत्त की त्रिज्या
= 2 × 3.5 cm
= 7 cm
∴ AC = BC = AB = 7 cm
तो, ΔABC एक समबाहु त्रिभुज है जिसकी भुजा 7 cm है।
हम जानते हैं कि, एक समबाहु त्रिभुज की दो आसन्न भुजाओं के बीच प्रत्येक कोण 60° का होता है।
∴ ∠A = 60° वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"A")/360^circ xx pi"r"^2`
= `60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
इसलिए, प्रत्येक त्रिज्यखंड का क्षेत्रफल = 3 × कोण A वाले त्रिज्यखंड का क्षेत्रफल
= `3 xx 60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
= `1/2 xx 22/7 xx 3.5 xx 3.5 "cm"^2`
= `11 xx 5/10 xx 35/10 "cm"^2`
= `77/4 "cm"^2`
= 19.25 cm2
और ΔABC का क्षेत्रफल = `sqrt(3)/4 xx (7)^2 "cm"^2` ...[∵ समबाहु त्रिभुज का क्षेत्रफल = `sqrt(3)/4 xx ("भुजा")^2 `]
= `(49sqrt(3))/4 "cm"^2`
∴ इन वृत्तों के बीच घिरे छायांकित क्षेत्र का क्षेत्रफल
= ΔABC का क्षेत्रफल – प्रत्येक त्रिज्यखंड का क्षेत्रफल
= `(49sqrt(3))/4 - 19.25`
= `12.25 xx sqrt(3) - 19.25`
= 21.2176 – 19.25
= 1.9676 cm2
अतः, इन वृत्तों के बीच घिरा आवश्यक क्षेत्रफल 1.967 cm2 (लगभग) है।
APPEARS IN
संबंधित प्रश्न
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है। `[pi = 22/7 "का प्रयोग करें"]`
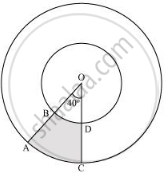
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृत्तों की त्रिज्याएँ क्रमश: 7 सेमी और 14 सेमी हैं तथा ∠AOC=40° है।
[Use Π = `22/7`]
यदि त्रिज्या r वाले एक वृत्त के एक चाप की लंबाई त्रिज्या 2r वाले एक वृत्त के चाप की लंबाई के बराबर हो, तो पहले वृत्त के संगत त्रिज्यखंड का कोण दूसरे वृत्त के संगत त्रिज्यखंड के कोण का दोग़ना होता है? क्या यह कथन असत्य है? क्यों?
दो भिन्न वृत्तों के दो त्रिज्यखंडों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन त्रिज्यखंडों के संगत चापों की लंबाइयाँ बराबर होंगी? क्यों?
त्रिज्या 14 cm वाले एक वृत्त के लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का कोण 60° है।
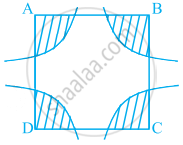
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
एक त्रिभुजाकार खेत की भुजाएँ 15 m, 16 m और 17 m हैं। इस खेत में चरने के लिए, इसके तीनों कोनों से एक गाय, एक भैंस और एक घोड़े को अलग-अलग 7 m लंबी रस्सियों से बाँध दिया गया है। खेत के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें ये तीनों पशु चर नहीं पाएँगे।
त्रिज्या 12 cm वाले वृत्त के उस वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का केंद्रीय कोण 60° है (π=3.14 का प्रयोग कीजिए)।
