Advertisements
Advertisements
प्रश्न
एक त्रिभुजाकार खेत की भुजाएँ 15 m, 16 m और 17 m हैं। इस खेत में चरने के लिए, इसके तीनों कोनों से एक गाय, एक भैंस और एक घोड़े को अलग-अलग 7 m लंबी रस्सियों से बाँध दिया गया है। खेत के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें ये तीनों पशु चर नहीं पाएँगे।
उत्तर
दिया गया है कि, एक त्रिकोणीय खेत जिसके तीन कोनों पर एक गाय, एक भैंस और एक घोड़ा अलग-अलग रस्सियों से बंधे हैं।
तो, प्रत्येक जानवर ने त्रिकोणीय क्षेत्र के प्रत्येक कोने में एक सेक्टर के रूप में खेत को चरा।
दिया गया है, प्रत्येक त्रिज्यखंड की त्रिज्या (r) = 7 m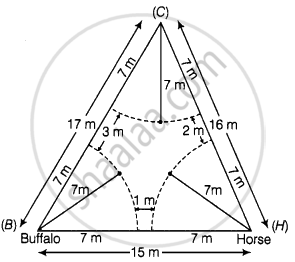
अब, ∠C वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"C")/360^circ xx pi"r"^2`
= `(∠"C")/360^circ xx pi xx (7)^2"m"^2`
∠B वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"B")/360^circ xx pi"r"^2`
= `(∠"B")/360^circ xx pi xx (7)^2"m"^2`
और ∠H वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"H")/360^circ xx pi"r"^2`
= `(∠"H")/360^circ xx pi xx (7)^2"m"^2`
इसलिए, तीन सेक्टरों के क्षेत्रफल का योग (cm2 में) है।
= `(∠"C")/360^circ xx pi xx (7)^2 + (∠"B")/360^circ xx pi xx (7)^2 + (∠"H")/360^circ xx pi xx (7)^2`
= `((∠"C" + ∠"B" + ∠"H"))/360^circ xx pi xx 49`
= `180^circ/360^circ xx 22/7 xx 49`
= 11 × 7
= 77 cm2
दिया गया है, त्रिभुज की भुजाएँ a = 15, b = 16 और c = 17 हैं।
अब, त्रिभुज की अर्ध-परिधि,
s = `("a" + "b" + "c")/2`
⇒ `(15 + 16 + 17)/2 = 48/2` = 24
∴ त्रिभुजाकार क्षेत्र का क्षेत्रफल
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))` ...[हेरॉन के सूत्र द्वारा]
= `sqrt(24 * 9 * 8* 7)`
= `sqrt(64 * 9 * 21)`
= `8 xx 3sqrt(21)`
= `24sqrt(21) "m"^2`
तो, खेत का वह क्षेत्र जो तीन जानवरों द्वारा नहीं चरा जा सकता है।
= त्रिकोणीय क्षेत्र का क्षेत्रफल – प्रत्येक क्षेत्रीय क्षेत्र का क्षेत्रफल
= `24sqrt(21) - 77 "m"^2`
अत:, खेत का आवश्यक क्षेत्रफल जिसे तीन जानवर नहीं चर सकते `(24sqrt(21) - 77) "m"^2` है।
APPEARS IN
संबंधित प्रश्न
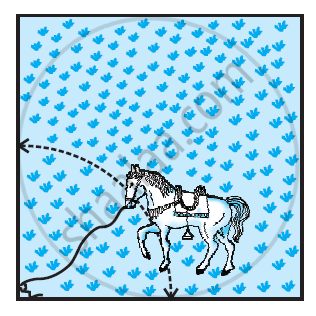
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है। ज्ञात कीजिए:
- मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
- चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए। [उपयोग = 3.14]
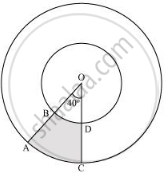
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृत्तों की त्रिज्याएँ क्रमश: 7 सेमी और 14 सेमी हैं तथा ∠AOC=40° है।
[Use Π = `22/7`]
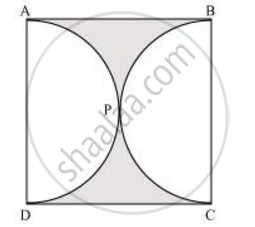
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं। [उपयोग Π = `22/7`]
व्यासों 36 cm और 20 cm वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या ______ है।
s मीटर की दूरी चलने के लिए, त्रिज्या r मीटर वाला एक वृत्ताकार पहिया `s/(2πr)` चक्कर लगाता है। क्या यह कथन सत्य है? क्यों?
किसी वृत्ताकार खेल के मैदान का क्षेत्रफल 22176 m2 है। इस मैदान पर 50 रु प्रति मीटर की दर से बाड़ लगवाने का व्यय ज्ञात कीजिए।
बराबर त्रिज्या 3.5 cm वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
त्रिज्या 5 cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई 3.5 cm है।
त्रिज्या 21 cm वाले एक वृत्त के 120∘ कोण वाले त्रिज्यखंड और उसके संगत दीर्घ त्रिज्यखंड के क्षेत्रफलों का अंतर ज्ञात कीजिए।
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत दीर्घ त्रिज्यखंड [प्रयोग कीजिए = 3.14]
