Advertisements
Advertisements
Question
एक त्रिभुजाकार खेत की भुजाएँ 15 m, 16 m और 17 m हैं। इस खेत में चरने के लिए, इसके तीनों कोनों से एक गाय, एक भैंस और एक घोड़े को अलग-अलग 7 m लंबी रस्सियों से बाँध दिया गया है। खेत के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें ये तीनों पशु चर नहीं पाएँगे।
Solution
दिया गया है कि, एक त्रिकोणीय खेत जिसके तीन कोनों पर एक गाय, एक भैंस और एक घोड़ा अलग-अलग रस्सियों से बंधे हैं।
तो, प्रत्येक जानवर ने त्रिकोणीय क्षेत्र के प्रत्येक कोने में एक सेक्टर के रूप में खेत को चरा।
दिया गया है, प्रत्येक त्रिज्यखंड की त्रिज्या (r) = 7 m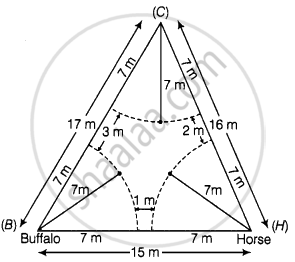
अब, ∠C वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"C")/360^circ xx pi"r"^2`
= `(∠"C")/360^circ xx pi xx (7)^2"m"^2`
∠B वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"B")/360^circ xx pi"r"^2`
= `(∠"B")/360^circ xx pi xx (7)^2"m"^2`
और ∠H वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"H")/360^circ xx pi"r"^2`
= `(∠"H")/360^circ xx pi xx (7)^2"m"^2`
इसलिए, तीन सेक्टरों के क्षेत्रफल का योग (cm2 में) है।
= `(∠"C")/360^circ xx pi xx (7)^2 + (∠"B")/360^circ xx pi xx (7)^2 + (∠"H")/360^circ xx pi xx (7)^2`
= `((∠"C" + ∠"B" + ∠"H"))/360^circ xx pi xx 49`
= `180^circ/360^circ xx 22/7 xx 49`
= 11 × 7
= 77 cm2
दिया गया है, त्रिभुज की भुजाएँ a = 15, b = 16 और c = 17 हैं।
अब, त्रिभुज की अर्ध-परिधि,
s = `("a" + "b" + "c")/2`
⇒ `(15 + 16 + 17)/2 = 48/2` = 24
∴ त्रिभुजाकार क्षेत्र का क्षेत्रफल
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))` ...[हेरॉन के सूत्र द्वारा]
= `sqrt(24 * 9 * 8* 7)`
= `sqrt(64 * 9 * 21)`
= `8 xx 3sqrt(21)`
= `24sqrt(21) "m"^2`
तो, खेत का वह क्षेत्र जो तीन जानवरों द्वारा नहीं चरा जा सकता है।
= त्रिकोणीय क्षेत्र का क्षेत्रफल – प्रत्येक क्षेत्रीय क्षेत्र का क्षेत्रफल
= `24sqrt(21) - 77 "m"^2`
अत:, खेत का आवश्यक क्षेत्रफल जिसे तीन जानवर नहीं चर सकते `(24sqrt(21) - 77) "m"^2` है।
APPEARS IN
RELATED QUESTIONS
6 सेमी त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60 डिग्री है। `[pi = 22/7 "का प्रयोग करें"]`
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए
चाप की लंबाई [प्रयोग कीजिए= `22/7`]
आकृति में, व्यास d वाले एक वृत्त के अंतर्गत एक वर्ग खींचा गया है तथा एक अन्य वर्ग इसी वृत्त के परिगत है। क्या बाहरी वर्ग का क्षेत्रफल आंतरिक वर्ग के क्षेत्रफल का चार गुना है? अपने उत्तर का कारण दीजिए।

उस वृत्त की त्रिज्या ज्ञात कीजिए, जिसकी परिधि त्रिज्याओं 15 cm और 18 cm वाले दो वृत्तों की परिधियों के योग के बराबर है।
त्रिज्या 28 cm वाले एक वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका केंद्रीय कोण 45° है।
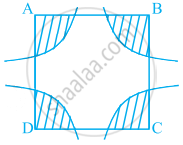
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हैं। इस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त का क्षेत्रफल 1256 cm2 है (π = 3.14 का प्रयोग कीजिए)।
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

त्रिज्या 21 cm वाले एक वृत्त के 120∘ कोण वाले त्रिज्यखंड और उसके संगत दीर्घ त्रिज्यखंड के क्षेत्रफलों का अंतर ज्ञात कीजिए।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल [ प्रयोग कीजिए =`22/7`]
