Advertisements
Advertisements
Question
किसी ट्रैक्टर के अगले और पिछले पहियों के व्यास क्रमशः 80 cm और 2m हैं। ज्ञात कीजिए कि पिछले पहिए द्वारा उतनी दूरी तय करने में कितने चक्कर लगाने होंगे, जितनी दूरी अगला पहिया 1400 चक्कर लगाने पर तय करता है।
Solution
प्रश्न के अनुसार,
अगले पहिये का व्यास = d1 = 80 cm
पिछले पहियों का व्यास = d2 = 2 m = 200 cm
मान लीजिए r1 अगले पहियों की त्रिज्या है = `80/2` = 40 cm
मान लीजिए r2 पिछले पहियों की त्रिज्या है = `200/2` = 100 cm
अब, आगे के पहियों की परिधि = 2πr
= `2 xx 22/7 xx 40`
= `1760/7` cm
पिछले पहियों की परिधि = 2πr
= `2 xx 22/7 xx 100`
= `4400/7` cm
अगले पहिये द्वारा किये गये चक्करों की संख्या = 1400
∴ अगले पहिये द्वारा तय की गई दूरी
= `1400 xx 1760/7`
= 352000 cm
किसी दूरी को तय करने में पीछे के पहिये द्वारा किए गए चक्करों की संख्या जिसमें सामने का पहिया 1400 चक्कर लगाता है।
= `"आगे के पहिये द्वारा तय की गई दूरी"/"पीछे के पहिये की परिधि"`
= `352000/(4400/7)`
= `(352000 xx 7)/4400`
= 560 चक्कर।
APPEARS IN
RELATED QUESTIONS
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
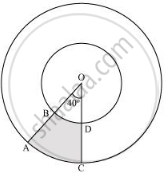
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृत्तों की त्रिज्याएँ क्रमश: 7 सेमी और 14 सेमी हैं तथा ∠AOC=40° है।
[Use Π = `22/7`]
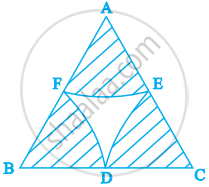
आकृति में, 10 cm भुजा वाले एक समबाहु त्रिभुज के शीर्षों A, B और C को केंद्र लेकर चाप खींचे गये हैं, जो परस्पर क्रमश: BC, CA और AB के मध्य बिंदुओं D, E और F पर प्रतिच्छेद करते हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
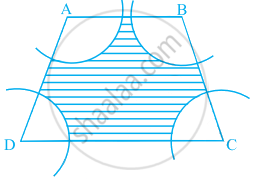
आकृति में, ABCD एक समलंब है, जिसमें AB || DC, AB = 18 cm, DC = 32 cm तथा AB और DC के बीच की दूरी = 14 cm है। यदि A, B, C और D को केंद्र मानकर त्रिज्याओं 7 cm के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
त्रिज्या 5 cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई 3.5 cm है।
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

किसी वृत्त के 200° केंद्रीय कोण वाले एक त्रिज्यखंड का क्षेत्रफल 770 cm2 है। इस त्रिज्यखंड के संगत चाप की लंबाई ज्ञात कीजिए।
वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई 5 cm है और जो केंद्र पर 90∘ का कोण अंतरित करती है।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल [प्रयोग कीजिए =`22/7`]
