Advertisements
Advertisements
Question
वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई 5 cm है और जो केंद्र पर 90∘ का कोण अंतरित करती है।
Solution

मान लीजिए कि वृत्त की त्रिज्या r है।
दिया गया है कि, एक वृत्त की जीवा की लंबाई, AB = 5 cm है।
और त्रिज्यखंड AOBA का केंद्रीय कोण (θ) = 90° है।
अब, ΔAOB में,
(AB)2 = (OA)2 + (OB)2 ...[पाइथागोरस प्रमेय द्वारा]
(5)2 = r2 + r2
⇒ 2r2 = 25
∴ r = `5/sqrt(2) "cm"`
अब, ΔAOB में हम एक लंब रेखा OD खींचते हैं, जो AB पर D पर मिलती है और जीवा AB को दो बराबर भागों में विभाजित करती है।
So, AD = DB
= `"AB"/2`
= `5/2 "cm"` ...[∵ वृत्त की जीवा पर केंद्र से खींचा गया लंब जीवा को दो बराबर भागों में विभाजित करता है।]
पाइथागोरस प्रमेय द्वारा, ΔADO में,
OA2 = OD2 + AD2
⇒ OD2 = OA2 – AD2
= `(5/sqrt(2))^2 - (5/2)^2`
= `25/2 - 25/4`
= `(50 - 25)/4`
= `25/4`
⇒ OD = `5/2 "cm"`
∴ एक समद्विबाहु ΔAOB का क्षेत्रफल
= `1/2 xx "AB" xx "OD"`
= `1/2 xx 5 xx 5/2`
= `25/4 "cm"^2`
अब, सेक्टर AOBA का क्षेत्रफल
= `(pi"r"^2)/360^circ xx θ`
= `(pi xx (5/sqrt(2))^2)/360^circ xx 90^circ`
= `(pi xx 25)/(2 xx 4)`
= `(25pi)/8 "cm"^2`
∴ लघु खण्ड का क्षेत्रफल
= त्रिज्यखंड AOBA का क्षेत्रफल – एक समद्विबाहु ΔAOB का क्षेत्रफल
= `((25pi)/8 - 25/4) "cm"^2`
अब, वृत्त का क्षेत्रफल
= πr2
= `pi(5/sqrt(2))^2`
= `(25pi)/2 "cm"^2`
∴ प्रमुख खण्ड का क्षेत्रफल
= वृत्त का क्षेत्रफल – लघु खण्ड का क्षेत्रफल
= `(25pi)/2 - ((25pi)/8 - 25/4)`
= `(25pi)/8 (4 - 1) + 25/4`
= `((75pi)/8 + 25/4) "cm"^2`
∴ एक वृत्त के दो खंडों के क्षेत्रफलों का अंतर
= प्रमुख खंड का क्षेत्रफल – लघु खंड का क्षेत्रफल
= `((75pi)/8 + 25/4) - ((25pi)/8 - 25/4)`
= `((75pi)/8 - (25pi)/8) + (25/4 + 25/4)`
= `(75pi - 25pi)/8 + 50/4`
= `(50pi)/8 + 50/4`
= `((25pi)/4 + 25/2) "cm"^2`
अतः, दो खंडों के क्षेत्रफलों का आवश्यक अंतर `((25pi)/4 + 25/2) "cm"^2` है।
APPEARS IN
RELATED QUESTIONS
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत लघु वृत्तखंड [प्रयोग कीजिए π = 3.14]
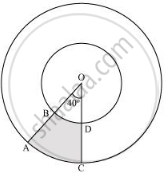
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृत्तों की त्रिज्याएँ क्रमश: 7 सेमी और 14 सेमी हैं तथा ∠AOC=40° है।
[Use Π = `22/7`]
क्या यह कहना सत्य है कि एक वृत्तखंड का क्षेत्रफल संगत त्रिज्यखंड के क्षेत्रफल से कम होता है? क्यों?
क्या यह कहना सत्य है कि व्यास d cm वाले एक वृत्ताकार पहिए द्वारा एक परिभ्रमण में चली गयी दूरी 2 π d cm होती है? क्यों?
एक वृत्त के क्षेत्रफल का संख्यात्मक मान उसकी परिधि के संख्यात्मक मान से अधिक होता है। क्या यह कथन सत्य है? क्यों?
दो भिन्न वृत्तों के दो त्रिज्यखंडों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन त्रिज्यखंडों के संगत चापों की लंबाइयाँ बराबर होंगी? क्यों?
दो वृत्तों के क्षेत्रफल बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों की परिधियाँ भी बराबर हों? क्यों?
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

किसी वृत्त के 200° केंद्रीय कोण वाले एक त्रिज्यखंड का क्षेत्रफल 770 cm2 है। इस त्रिज्यखंड के संगत चाप की लंबाई ज्ञात कीजिए।
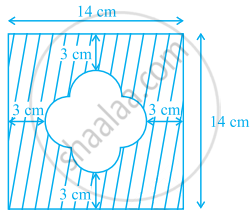
आकृति में, दिये छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।