Advertisements
Advertisements
Question
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

Solution
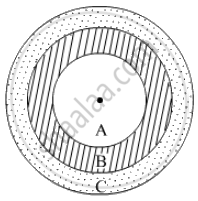
माना कि तीन क्षेत्र A, B और C हैं।
व्यास 1 : 2 : 3 के अनुपात में हैं।
मान लीजिए कि व्यास 1x, 2x और 3x हैं।
तब त्रिज्या होगी `x/2, (2x)/2` और `(3x)/2`
क्षेत्र A का क्षेत्रफल = `pi"r"_"A"^2`
= `pi(x/2)^2`
= `pix^2/4`
क्षेत्र B का क्षेत्रफल = `pi"r" _"B"^2-pi"r" _"A"^2`
= `pi(x)^2-pi(x/2)^2`
= `(3pi(x)^2)/4`
क्षेत्र C का क्षेत्रफल = `pi"r"_"C"^2-pi"r"_"B"^2-pi"r"_"A"^2`
= `pi((3x)/2)^2-pi(x)^2-pi(x/2)^2`
= `pi((3x)/2)^2-(3pix^2)/4`
= `(5pix^2)/4`
इस प्रकार, क्षेत्र A, B और C के क्षेत्रफलों का अनुपात होगा
`pix^2/4 : (3pi(x)^2)/4 : (5pix^2)/4`
⇒ 1 : 3 : 5
APPEARS IN
RELATED QUESTIONS
आकृति में, व्यास d वाले एक वृत्त के अंतर्गत एक वर्ग खींचा गया है तथा एक अन्य वर्ग इसी वृत्त के परिगत है। क्या बाहरी वर्ग का क्षेत्रफल आंतरिक वर्ग के क्षेत्रफल का चार गुना है? अपने उत्तर का कारण दीजिए।

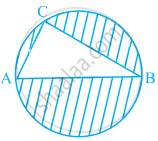
आकृति में, AB वृत का व्यास है, AC = 6 cm और BC = 8 cm है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
एक वृत्ताकार पार्क के अनुदिश बाहर की ओर 21 m चौड़ी एक सड़क है। यदि पार्क की त्रिज्या 105 m है, तो सड़क का क्षेत्रफल ज्ञात कीजिए।
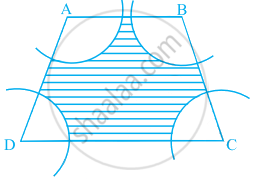
आकृति में, ABCD एक समलंब है, जिसमें AB || DC, AB = 18 cm, DC = 32 cm तथा AB और DC के बीच की दूरी = 14 cm है। यदि A, B, C और D को केंद्र मानकर त्रिज्याओं 7 cm के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
त्रिज्या 5 cm वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई 3.5 cm है।
एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हैं। इस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त का क्षेत्रफल 1256 cm2 है (π = 3.14 का प्रयोग कीजिए)।
त्रिज्याओं 7 cm और 21 cm वाले दो वृत्तों के दो त्रिज्यखंडों के केंद्रीय कोण क्रमशः 120∘ और 40∘ हैं। इन दोनों त्रिज्यखंडों के क्षेत्रफल तथा साथ ही संगत चापों की लंबाई ज्ञात कीजिए। आप क्या देखते हैं?
त्रिज्या 21 cm वाले एक वृत्त के 120∘ कोण वाले त्रिज्यखंड और उसके संगत दीर्घ त्रिज्यखंड के क्षेत्रफलों का अंतर ज्ञात कीजिए।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल [ प्रयोग कीजिए =`22/7`]
