Advertisements
Advertisements
Question
एक वृत्ताकार पार्क के अनुदिश बाहर की ओर 21 m चौड़ी एक सड़क है। यदि पार्क की त्रिज्या 105 m है, तो सड़क का क्षेत्रफल ज्ञात कीजिए।
Solution
वृत्ताकार सड़क और पार्क संकेंद्रित वृत्त हैं।
पार्क की त्रिज्या = r1 = 105 m
सड़क की चौड़ाई = 21 m
वृत्ताकार सड़क और पार्क की त्रिज्या = r2
= 105 m + 21 m
= 126 m
तो, सड़क का क्षेत्रफल = पार्क का क्षेत्रफल और सड़क – पार्क का क्षेत्रफल
= `π"r"_2^2 - π"r"_1^2`
= `π["r"_2^2 - "r"_1^2]`
= `22/7 [(126)^2 - (105)^2]`
= `22/7 [126 - 105][126 + 105]`
= `22/7 xx 21 xx 231`
= 22 × 3 × 231
= 66 × 231
= 15246 cm2
∴ सड़क का क्षेत्रफल = 15246 cm2
APPEARS IN
RELATED QUESTIONS
दो भिन्न वृत्तों के बराबर लंबाइयों वाले चापों के संगत त्रिज्यखंडों के क्षेत्रफल बराबर होते हैं। क्या यह कथन सत्य है? क्यों?
दो वृत्तों की परिधियाँ बराबर हैं। क्या यह आवश्यक है कि इन वृतों के क्षेत्रफल भी बराबर हों? क्यों?
त्रिज्या 28 cm वाले एक वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका केंद्रीय कोण 45° है।
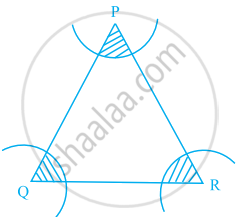
आकृति में, 14 cm की त्रिज्याएँ लेकर तथा P, Q और R को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
एक 20 cm लंबे तार के टुकड़े को मोड़कर एक वृत्त का चाप बनाया गया है, जो इस वृत्त के केंद्र पर 60° का कोण अंतरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
एक त्रिभुजाकार खेत की भुजाएँ 15 m, 16 m और 17 m हैं। इस खेत में चरने के लिए, इसके तीनों कोनों से एक गाय, एक भैंस और एक घोड़े को अलग-अलग 7 m लंबी रस्सियों से बाँध दिया गया है। खेत के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें ये तीनों पशु चर नहीं पाएँगे।
त्रिज्या 12 cm वाले वृत्त के उस वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का केंद्रीय कोण 60° है (π=3.14 का प्रयोग कीजिए)।
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल [प्रयोग कीजिए =`22/7`]
