Advertisements
Advertisements
Question
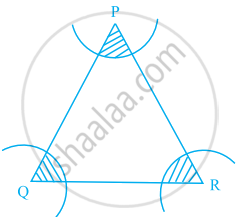
आकृति में, 14 cm की त्रिज्याएँ लेकर तथा P, Q और R को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution
दिया गया है, प्रत्येक चाप की त्रिज्या (r) = 14 cm
अब, केंद्रीय कोण P वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"P")/360^circ xx π"r"^2`
= `(∠"P")/360^circ xx π xx (14)^2 "cm"^2`
केंद्रीय कोण Q वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"Q")/360^circ xx π"r"^2`
= `(∠"Q")/360^circ xx π xx (14)^2 "cm"^2`
और केंद्रीय कोण R वाले त्रिज्यखंड का क्षेत्रफल
= `(∠"R")/360^circ xx π"r"^2`
= `(∠"R")/360^circ xx π xx (14)^2 "cm"^2`
इसलिए, तीन क्षेत्रों के क्षेत्रों का योग
= `(∠"P")/360^circ xx π xx (14)^2 + (∠"Q")/360^circ xx π xx (14)^2 + (∠"R")/360^circ xx π xx (14)^2`
= `π/360^circ xx (14)^2 xx [∠"P" + ∠"Q" + ∠"R"]`
= `π/360^circ xx 196 xx 180^circ` ...[चूँकि, किसी भी त्रिभुज के सभी आंतरिक कोणों का योग 180° होता है।]
= 98π
= `98 xx 22/7`
= 14 × 22
= 308
अतः, छायांकित क्षेत्र का आवश्यक क्षेत्रफल 308 cm2 है।
APPEARS IN
RELATED QUESTIONS
15 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 60° का कोण अंतरित करती है। वृत्त के संगत लघु और प्रमुख खण्डों के क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73`]
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
व्यासों 36 cm और 20 cm वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या ______ है।
क्या यह कहना सत्य है कि व्यास d cm वाले एक वृत्ताकार पहिए द्वारा एक परिभ्रमण में चली गयी दूरी 2 π d cm होती है? क्यों?
एक वृत्ताकार पार्क के अनुदिश बाहर की ओर 21 m चौड़ी एक सड़क है। यदि पार्क की त्रिज्या 105 m है, तो सड़क का क्षेत्रफल ज्ञात कीजिए।
एक 20 cm लंबे तार के टुकड़े को मोड़कर एक वृत्त का चाप बनाया गया है, जो इस वृत्त के केंद्र पर 60° का कोण अंतरित करता है। वृत्त की त्रिज्या ज्ञात कीजिए।
त्रिज्या 12 cm वाले वृत्त के उस वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का केंद्रीय कोण 60° है (π=3.14 का प्रयोग कीजिए)।
किसी कमरे के फर्श की विमाएँ 5 m × 4 m हैं और इस पर वृत्ताकार टाइलें लगायी जाती हैं, जिनमें से प्रत्येक का व्यास 50 cm है, जैसा कि आकृति में दर्शाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर टाइल नहीं लगी हैं (π = 3.14 का प्रयोग कीजिए)।

एक घड़ी की मिनट वाली सुई की लंबाई 5 cm है। प्रात: 6 : 05 बजे से प्रातः 6 : 40 बजे तक के समय काल में इस सुई द्वारा तय किये गये (या घूमे गये) क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
किसी वृत्त के 200° केंद्रीय कोण वाले एक त्रिज्यखंड का क्षेत्रफल 770 cm2 है। इस त्रिज्यखंड के संगत चाप की लंबाई ज्ञात कीजिए।
