Advertisements
Advertisements
Question
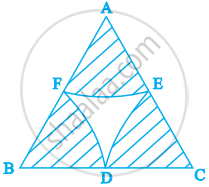
आकृति में, 10 cm भुजा वाले एक समबाहु त्रिभुज के शीर्षों A, B और C को केंद्र लेकर चाप खींचे गये हैं, जो परस्पर क्रमश: BC, CA और AB के मध्य बिंदुओं D, E और F पर प्रतिच्छेद करते हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
Solution
चूँकि, ΔABC एक समबाहु त्रिभुज है।
∴ ∠A = ∠B = ∠C = 60°
और AB = BC = CA = 10 cm
E, F और D दी गई भुजाओं के मध्य-बिंदु हैं।
∴ AE = EC = CD = DB = BF = FA = 5 cm
त्रिज्यखंड की त्रिज्या (r) = 5 cm
अब, सेक्टर CDE का क्षेत्रफल
= `θ/360^circ xx π"r"^2`
= `60^circ/360^circ xx 3.14 xx (5)^2 "cm"^2`
= `(3.14 xx 25)/6 "cm"^2`
= `78.5/6 "cm"^2`
= 13.0833 cm2
∴ छायांकित क्षेत्र का क्षेत्रफल
= 3 (सेक्टर सीडीई का क्षेत्रफल)
= 3 × 13.0833 cm2
= 39.25 cm2
APPEARS IN
RELATED QUESTIONS
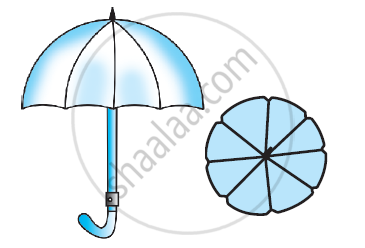
एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं। छतरी को 45 सेमी त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
व्यासों 36 cm और 20 cm वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या ______ है।
यदि त्रिज्या r वाले एक वृत्त के एक चाप की लंबाई त्रिज्या 2r वाले एक वृत्त के चाप की लंबाई के बराबर हो, तो पहले वृत्त के संगत त्रिज्यखंड का कोण दूसरे वृत्त के संगत त्रिज्यखंड के कोण का दोग़ना होता है? क्या यह कथन असत्य है? क्यों?
किसी वृत्ताकार खेल के मैदान का क्षेत्रफल 22176 m2 है। इस मैदान पर 50 रु प्रति मीटर की दर से बाड़ लगवाने का व्यय ज्ञात कीजिए।
एक समचतुर्भुज के सभी शीर्ष एक वृत्त पर स्थित हैं। इस समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त का क्षेत्रफल 1256 cm2 है (π = 3.14 का प्रयोग कीजिए)।
वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई 5 cm है और जो केंद्र पर 90∘ का कोण अंतरित करती है।
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
संगत दीर्घ त्रिज्यखंड [प्रयोग कीजिए = 3.14]
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल [प्रयोग कीजिए =`22/7`]
