Advertisements
Advertisements
Question
किसी कमरे के फर्श की विमाएँ 5 m × 4 m हैं और इस पर वृत्ताकार टाइलें लगायी जाती हैं, जिनमें से प्रत्येक का व्यास 50 cm है, जैसा कि आकृति में दर्शाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर टाइल नहीं लगी हैं (π = 3.14 का प्रयोग कीजिए)।

Solution
दिया गया है, एक कमरे का फर्श गोलाकार टाइलों से ढका हुआ है।
एक कमरे के फर्श की लंबाई (l) = 5 m
और एक कमरे के फर्श की चौड़ाई (b) = 4 m
∴ कमरे के फर्श का क्षेत्रफल = l × b
= 5 × 4
= 20 m2
⇒ प्रत्येक वृत्ताकार टाइल की त्रिज्या (r) = `50/2 "cm"`
= 25 m
= `25/100 "m"`
= `1/4 "m"`
अब, एक वृत्ताकार टाइल का क्षेत्रफल = πr2
= `3.14 xx (1/4)^2 "m"^2`
= `3.14/16 "m"^2`
∴ वृत्ताकार टाइलों की संख्या = 80
∴ 80 वृत्ताकार टाइलों का क्षेत्रफल
= `80 xx 3.14/16`
= 5 × 3.14
= 15.7 m2
तो, टाइलों से ढके फर्श का क्षेत्रफल = एक कमरे के फर्श का क्षेत्रफल – 80 गोलाकार टाइलों का क्षेत्रफल
= 20 – 15.7
= 4.3 m2
अतः, टाइलों से ढके फर्श का आवश्यक क्षेत्रफल 4.3 cm2 है।
APPEARS IN
RELATED QUESTIONS
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है। `[pi = 22/7 "का प्रयोग करें"]`
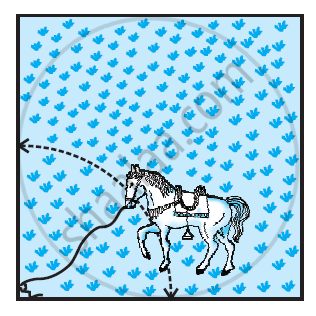
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है। ज्ञात कीजिए:
- मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
- चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए। [उपयोग = 3.14]
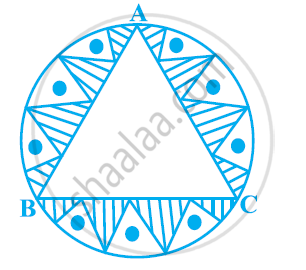
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु ABC त्रिभुज छोड़ते हुए एक डिजाइनर बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
व्यासों 36 cm और 20 cm वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या ______ है।
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
आकृति में, 14 cm की त्रिज्याएँ लेकर तथा P, Q और R को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
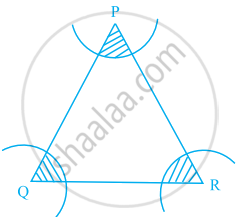
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
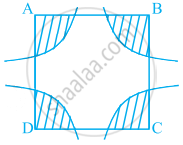
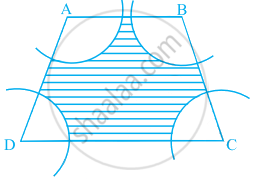
आकृति में, ABCD एक समलंब है, जिसमें AB || DC, AB = 18 cm, DC = 32 cm तथा AB और DC के बीच की दूरी = 14 cm है। यदि A, B, C और D को केंद्र मानकर त्रिज्याओं 7 cm के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

