Advertisements
Advertisements
Question
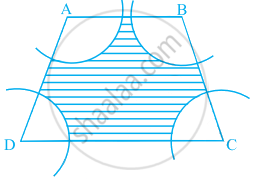
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
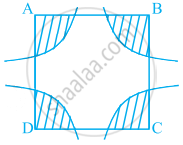
Solution
दिया गया है कि, प्रत्येक चाप की त्रिज्या (r) = 21 cm
∠A के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"A")/360^circ xx π"r"^2`
= `(∠"A")/360^circ xx π xx (21)^2 "cm"^2`
∠B के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"B")/360^circ xx π"r"^2`
= `(∠"B")/360^circ xx π xx (21)^2 "cm"^2`
∠C के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"C")/360^circ xx π"r"^2`
= `(∠"C")/360^circ xx π xx (21)^2 "cm"^2`
और ∠D के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"D")/360^circ xx π"r"^2`
= `(∠"D")/360^circ xx π xx (21)^2 "cm"^2`
इसलिए, चारों सेक्टरों के क्षेत्रफलों का योग (cm2 में) है।
= `(∠"A")/360^circ xx π xx (21)^2 + (∠"B")/360^circ xx π xx (21)^2 + (∠"C")/360^circ xx π xx (21)^2 + (∠"D")/360^circ xx π xx (21)^2`
= `π/360^circ xx (21)^2 xx [∠"A" + ∠"B" + ∠"C" + ∠"D"]`
= `π/360^circ xx (21)^2 xx 360^circ` ...[∵ एक चतुर्भुज में सभी आंतरिक कोणों का योग = 360°]
= `22/7 xx 21 xx 21`
= 22 × 3 × 21
= 1386
अतः, छायांकित क्षेत्र का आवश्यक क्षेत्रफल 1386 cm2 है।
APPEARS IN
RELATED QUESTIONS
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है। `[pi = 22/7 "का प्रयोग करें"]`
12 सेमी त्रिज्या वाले वृत्त की एक जीवा केंद्र पर 120° का कोण अंतरित करती है। वृत्त के संगत वृत्त खण्ड का क्षेत्रफल ज्ञात कीजिए। [π = 3.14 और `sqrt3 = 1.73 ` का प्रयोग कीजिए।]
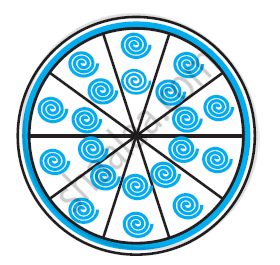
एक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल [उपयोग π = `22/7`]
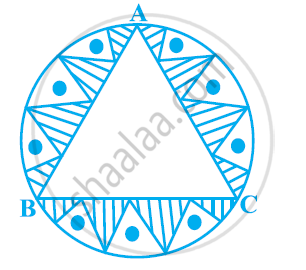
एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 सेमी है, में बीच में एक समबाहु ABC त्रिभुज छोड़ते हुए एक डिजाइनर बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए। [उपयोग Π = 22/7]
यदि त्रिज्या r वाले एक वृत्त के एक चाप की लंबाई त्रिज्या 2r वाले एक वृत्त के चाप की लंबाई के बराबर हो, तो पहले वृत्त के संगत त्रिज्यखंड का कोण दूसरे वृत्त के संगत त्रिज्यखंड के कोण का दोग़ना होता है? क्या यह कथन असत्य है? क्यों?
दो भिन्न वृत्तों के बराबर लंबाइयों वाले चापों के संगत त्रिज्यखंडों के क्षेत्रफल बराबर होते हैं। क्या यह कथन सत्य है? क्यों?
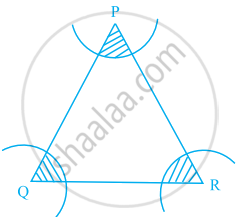
आकृति में, 14 cm की त्रिज्याएँ लेकर तथा P, Q और R को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
आकृति में, ABCD एक समलंब है, जिसमें AB || DC, AB = 18 cm, DC = 32 cm तथा AB और DC के बीच की दूरी = 14 cm है। यदि A, B, C और D को केंद्र मानकर त्रिज्याओं 7 cm के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
किसी वृत्त के 200° केंद्रीय कोण वाले एक त्रिज्यखंड का क्षेत्रफल 770 cm2 है। इस त्रिज्यखंड के संगत चाप की लंबाई ज्ञात कीजिए।
