Advertisements
Advertisements
Question
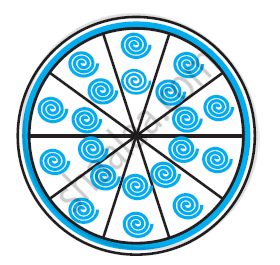
एक वृत्ताकार ब्रूच को चाँदी के तार से बनाया जाना है जिसका व्यास 35 मिमी है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल [उपयोग π = `22/7`]
Solution
आवश्यक तार की कुल लंबाई 5 व्यास की लंबाई और ब्रोच की परिधि होगी।
वृत्त की त्रिज्या = `35/2` mm
ब्रोच की परिधि = 2πr
`= 2 xx 22/7xx (35/2)`
= 110 mm
तार की लंबाई आवश्यक = 110 + 5 × 35
= 110 + 175
= 285 mm
चित्र से यह देखा जा सकता है कि वृत्त के 10 त्रिज्यखंडों में से प्रत्येक वृत्त के केंद्र पर 36° अंतरित कर रहा है
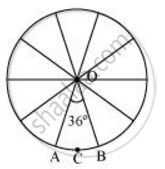
इसलिए, प्रत्येक क्षेत्र का क्षेत्रफल
= `36^@/360^@ xx pir^2`
`=1/10xx22/7xx(35/2)xx(35/2)`
= `385/4` mm2
APPEARS IN
RELATED QUESTIONS
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है। `[pi = 22/7 "का प्रयोग करें"]`
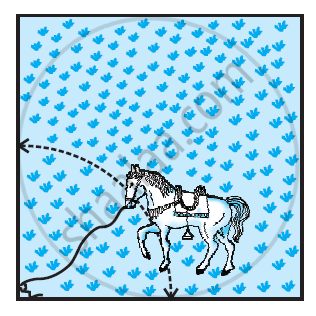
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है। ज्ञात कीजिए:
- मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
- चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए। [उपयोग = 3.14]
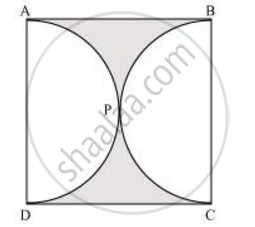
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 सेमी का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं। [उपयोग Π = `22/7`]
यदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो ______।
क्या यह कहना सत्य है कि एक वृत्तखंड का क्षेत्रफल संगत त्रिज्यखंड के क्षेत्रफल से कम होता है? क्यों?
यदि त्रिज्या r वाले एक वृत्त के एक चाप की लंबाई त्रिज्या 2r वाले एक वृत्त के चाप की लंबाई के बराबर हो, तो पहले वृत्त के संगत त्रिज्यखंड का कोण दूसरे वृत्त के संगत त्रिज्यखंड के कोण का दोग़ना होता है? क्या यह कथन असत्य है? क्यों?
उस वृत्त की त्रिज्या ज्ञात कीजिए, जिसकी परिधि त्रिज्याओं 15 cm और 18 cm वाले दो वृत्तों की परिधियों के योग के बराबर है।
आकृति में, 10 cm भुजा वाले एक समबाहु त्रिभुज के शीर्षों A, B और C को केंद्र लेकर चाप खींचे गये हैं, जो परस्पर क्रमश: BC, CA और AB के मध्य बिंदुओं D, E और F पर प्रतिच्छेद करते हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए (π = 3.14 का प्रयोग कीजिए)।
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

एक घड़ी की मिनट वाली सुई की लंबाई 5 cm है। प्रात: 6 : 05 बजे से प्रातः 6 : 40 बजे तक के समय काल में इस सुई द्वारा तय किये गये (या घूमे गये) क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
