Advertisements
Advertisements
प्रश्न
आकृति में, चतुर्भुज ABCD के A, B, C और D शीर्षों को केंद्र मानकर और 21 cm की त्रिज्या लेकर चाप खींचें गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
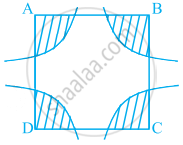
उत्तर
दिया गया है कि, प्रत्येक चाप की त्रिज्या (r) = 21 cm
∠A के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"A")/360^circ xx π"r"^2`
= `(∠"A")/360^circ xx π xx (21)^2 "cm"^2`
∠B के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"B")/360^circ xx π"r"^2`
= `(∠"B")/360^circ xx π xx (21)^2 "cm"^2`
∠C के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"C")/360^circ xx π"r"^2`
= `(∠"C")/360^circ xx π xx (21)^2 "cm"^2`
और ∠D के साथ त्रिज्यखंड का क्षेत्रफल
= `(∠"D")/360^circ xx π"r"^2`
= `(∠"D")/360^circ xx π xx (21)^2 "cm"^2`
इसलिए, चारों सेक्टरों के क्षेत्रफलों का योग (cm2 में) है।
= `(∠"A")/360^circ xx π xx (21)^2 + (∠"B")/360^circ xx π xx (21)^2 + (∠"C")/360^circ xx π xx (21)^2 + (∠"D")/360^circ xx π xx (21)^2`
= `π/360^circ xx (21)^2 xx [∠"A" + ∠"B" + ∠"C" + ∠"D"]`
= `π/360^circ xx (21)^2 xx 360^circ` ...[∵ एक चतुर्भुज में सभी आंतरिक कोणों का योग = 360°]
= `22/7 xx 21 xx 21`
= 22 × 3 × 21
= 1386
अतः, छायांकित क्षेत्र का आवश्यक क्षेत्रफल 1386 cm2 है।
APPEARS IN
संबंधित प्रश्न
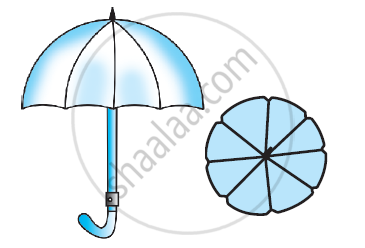
एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं। छतरी को 45 सेमी त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
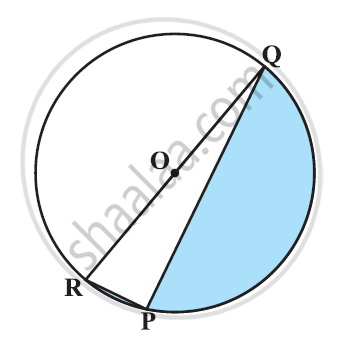
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 सेमी, PR = 7 सेमी तथा O वृत्त का केंद्र है। [उपयोग Π = `22/7`]
विमाओं 20 m × 16 m वाले एक आयताकार खेत के कोने पर एक गाय 14 m लंबी रस्सी से बँधी हुई है। खेत का वह क्षेत्रफल ज्ञात कीजिए जिसमें गाय चर सकती है।
एक वृत्ताकार पार्क के अनुदिश बाहर की ओर 21 m चौड़ी एक सड़क है। यदि पार्क की त्रिज्या 105 m है, तो सड़क का क्षेत्रफल ज्ञात कीजिए।
बराबर त्रिज्या 3.5 cm वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
किसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो आकृति में दर्शाए अनुसार तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1 : 2 : 3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।

एक घड़ी की मिनट वाली सुई की लंबाई 5 cm है। प्रात: 6 : 05 बजे से प्रातः 6 : 40 बजे तक के समय काल में इस सुई द्वारा तय किये गये (या घूमे गये) क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई 5 cm है और जो केंद्र पर 90∘ का कोण अंतरित करती है।
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए।
संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल [ प्रयोग कीजिए =`22/7`]
